What you will learn in the blog:
- What is Dynamic Programming?
- Why is Dynamic Programming Important?
- Step-by-Step Guide to Solving DP Problems
- Top-Down and Bottom-Up Approaches in Dynamic Programming
- Dynamic Programming Examples
- Applications of Dynamic Programming
- Common Challenges and How to Overcome Them
- Conclusion
- Frequently Asked Questions
Dynamic programming (DP) may sound complex, but it’s a powerful technique for tackling optimization and recursion problems. Essentially, it helps break a problem into smaller subproblems, solving each once and storing the results. If you’ve been exploring problem-solving techniques, you’ll find DP a game-changer once you simplify it. Let’s dive in and make it easy to understand, step by step.
Also Read: Beginner’s Guide to Lua Coding
What is Dynamic Programming?
Dynamic programming is a problem-solving technique used in algorithms. At its core, DP is about reusing past results to avoid redundant calculations.
“The best way to predict the future is to implement it, algorithmically.”
– Alan Kay
The key principles of dynamic programming are:
1. Optimal Substructure: This means that the best solution to a problem can be built by combining the best solutions to its smaller subproblems. Think of it like solving a puzzle, where each piece is crucial to the bigger picture.
2. Overlapping Subproblems: Unlike divide-and-conquer problems where each subproblem is unique, DP problems keep revisiting the same subproblems. It’s like solving the same mini-puzzles multiple times, which is why caching results can save a lot of time.
Why is Dynamic Programming Important?
According to a study by IEEE, implementing DP in optimization problems reduced computational costs by up to 40% in systems with high-dimensional data. In practical terms, this means faster processing times and better resource utilization.
Step-by-Step Guide to Solving DP Problems
Here’s a step-by-step guide to help you approach DP problems. Expand each section below to dive into each step and build a strong foundation in dynamic programming.
- Break it down into smaller, manageable parts: Identify the subproblems within the main problem.
- Look for overlapping subproblems: These are repeated subproblems that can be solved once and reused.
- Check for optimal substructure: Verify if the problem’s solution can be constructed from the solutions of smaller subproblems.
- Define how the larger problem can be broken down into smaller subproblems. The recurrence relation expresses this relationship mathematically or logically.
- Identify base cases: Before solving the recurrence relation, determine the simplest subproblems (base cases) and their solutions to prevent infinite recursion.
- Top-Down (Memoization): Break down the problem recursively, storing solutions to subproblems (typically using recursion with a cache).
- Bottom-Up (Tabulation): Solve all subproblems iteratively, starting from the smallest ones and building up to the final solution.
- Consider hybrid approaches: In some cases, it may be beneficial to combine top-down and bottom-up strategies or make optimizations (e.g., reduce space complexity).
- Use arrays or hashmaps for storing subproblem solutions: Ensure that you store the results of each subproblem to avoid redundant calculations.
- Optimize space: Use space-efficient data structures, and minimize the storage of unnecessary information.
- Optimize time complexity: After implementing, analyze the time complexity of your solution to ensure it meets the problem’s constraints.
- Test with different inputs: Ensure your solution works for edge cases, such as very small or very large inputs.
- Refine the solution: After testing, optimize your solution for better efficiency, if possible (e.g., by reducing time complexity or memory usage).
Top-Down and Bottom-Up Approaches in Dynamic Programming
When tackling dynamic programming problems, you’ll encounter two main approaches: Top-Down (Memoization) and Bottom-Up (Tabulation).
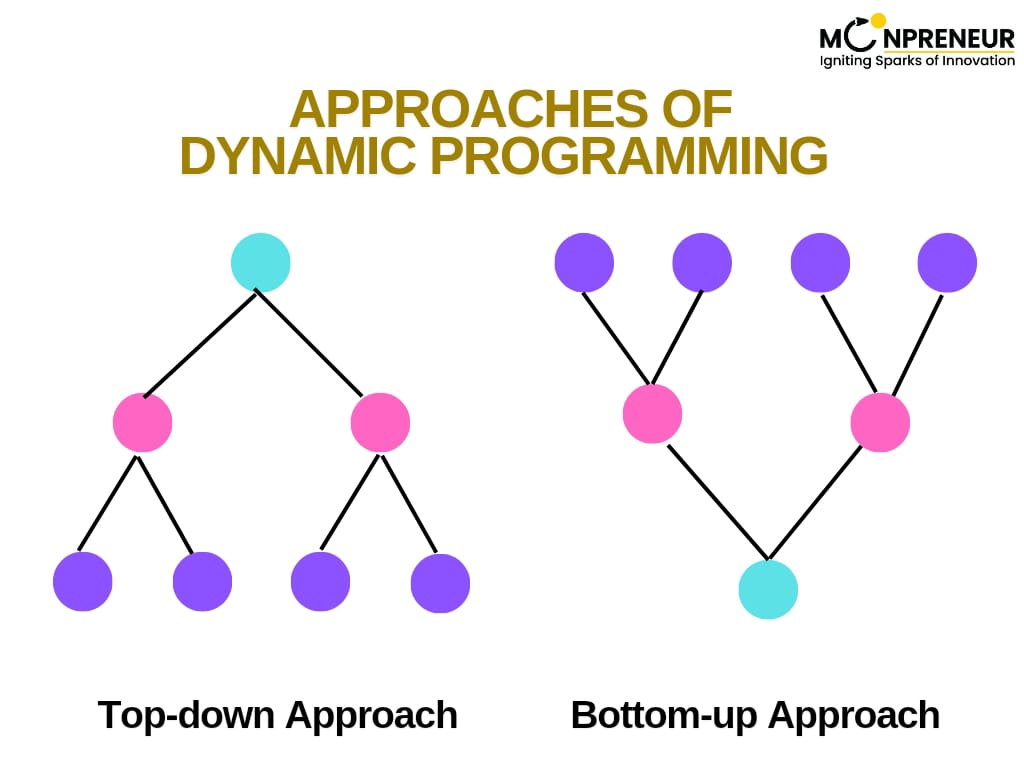
1. Top-Down (Memoization)
Think of this as solving a puzzle step-by-step, but storing the solutions to smaller pieces as you go, so you don’t repeat the same work. It’s intuitive but can use extra memory due to recursion.
2. Bottom-Up (Tabulation)
This method starts small and builds the solution iteratively. It’s more efficient in terms of memory, but might require a bit more effort to set up.
Dynamic Programming Examples
Let’s explore a couple of classic DP problems and how we can solve them using this approach.
1. Fibonacci Sequence
The Fibonacci sequence is a classic example of dynamic programming. Each number is the sum of the two preceding ones.
Recurrence Relation:
Base Cases:
Tabulation Approach:
fib = [0] * (n + 1) # Create an array to store Fibonacci numbers
fib[1] = 1 # Base case: F(1) = 1
for i in range(2, n + 1):
fib[i] = fib[i-1] + fib[i-2] # Fill the array iteratively
print(fib[n]) # Output the 10th Fibonacci number
2. Knapsack Problem
You have a set of items with weights and values, and a knapsack with a weight limit. The goal is to maximize the total value while staying within the weight limit.
Recurrence Relation:
If the item’s weight is less than or equal to the remaining capacity, choose the maximum between including and excluding the item.
Base Cases:
If no items are left or if the knapsack has no capacity, the value is 0.
Applications of Dynamic Programming
Dynamic programming is used in many fields:
- Bioinformatics: Sequence alignment and genome assembly.
- Machine Learning: Training algorithms and predictive modeling.
- Operations Research: Resource allocation and inventory management.
Real-World Example: Shortest Path Problem
Google Maps uses DP to calculate the shortest route from your location to the destination. The algorithm evaluates overlapping subproblems (various paths) and constructs the optimal path by storing intermediate results.
“Dynamic programming is not about programming in the coding sense; it’s about planning your computational steps dynamically.”
– Richard Bellman, Creator of DP
Common Challenges and How to Overcome Them
| Challenge | Solution |
|---|---|
| Identifying DP Problems | Practice recognizing overlapping subproblems. Start by solving simple problems like the Fibonacci sequence, where you can clearly see the repeated calculations. Gradually move on to more complex problems to build recognition skills. |
| Writing Recurrence Relations | Start with simple examples like Fibonacci or the Knapsack problem. Break down the problem into smaller subproblems and try to find how each subproblem relates to the whole. As you progress, tackle more complex problems and refine your recurrence relations. |
| Choosing Between Memoization and Tabulation | Understand the problem’s structure. If the problem involves recursion with overlapping subproblems, memoization (top-down) is useful. For problems where you can iteratively solve smaller subproblems, tabulation (bottom-up) is more efficient. |
| Handling Large Inputs | Optimize space and time complexity. Use space optimization techniques, like storing only the previous row in a DP table (for problems like Fibonacci), and analyze time complexity to avoid inefficient solutions. |
| Debugging DP Solutions | Work through examples step by step. For complex problems, manually trace through the algorithm with small inputs to identify where things go wrong. Print intermediate results to verify each step. |
| Avoiding Redundant Calculations | Use memoization or tabulation. Storing intermediate results ensures that each subproblem is solved only once, preventing redundant work and improving efficiency. |
Conclusion
Dynamic programming is a game-changer in problem-solving, allowing you to tackle complex challenges with efficiency. By mastering its core principles and practicing with problems like Fibonacci and the knapsack, you’ll gain the skills to optimize your solutions. Start simple, then challenge yourself with advanced problems like coin change. Have you figured out how to improve time complexity? Share your thoughts and solutions in the comments – we’d love to hear from you!
Moonpreneur is on a mission to disrupt traditional education and future-proof the next generation with holistic learning solutions. Its Innovator Program is building tomorrow’s workforce by training students in AI/ML, Robotics, Coding, IoT, and Apps, enabling entrepreneurship through experiential learning.
Frequently Asked Questions
Dynamic programming is a method used to solve complex problems by breaking them down into smaller, manageable subproblems. It stores the results of subproblems to avoid redundant computations, improving efficiency.
Dynamic programming is effective for optimization problems with overlapping subproblems and an optimal substructure, like the Knapsack Problem and Fibonacci Sequence.
Both recursion and dynamic programming break down a problem into smaller subproblems. However, dynamic programming stores the results of these subproblems to avoid recalculating them, making it more efficient.
A problem must have:
- Overlapping subproblems: These subproblems are solved multiple times during the computation.
- Optimal substructure: The solution to the problem can be derived from the solutions of its subproblems.
- Top-down (Memoization): Recursively solve the problem and store the results for reuse.
- Bottom-up (Tabulation): Iteratively solve subproblems, building up to the final solution.
To solve DP problems:
- Check if the problem has overlapping subproblems and optimal substructure.
- Define the recurrence relation and base cases.
- Choose between memoization or tabulation based on the problem.
- Analyze time complexity.
