
The concept of the magnitude of a vector plays a key role in mathematics and is widely used in coordinate geometry, physics, engineering, and even competitive exams. Knowing how to calculate vector magnitude helps students solve problems involving length, displacement, velocity, and force quickly and accurately.
What Is the Magnitude of a Vector?
The magnitude of a vector is the “length” or “size” of the vector irrespective of its direction. It tells us how much of the quantity is present.
👉 Example: If force is a vector, its magnitude represents the strength of the force.
This concept is commonly used in vector algebra, components of vectors, and real-world physics problems.
Key Formula for Magnitude of a Vector
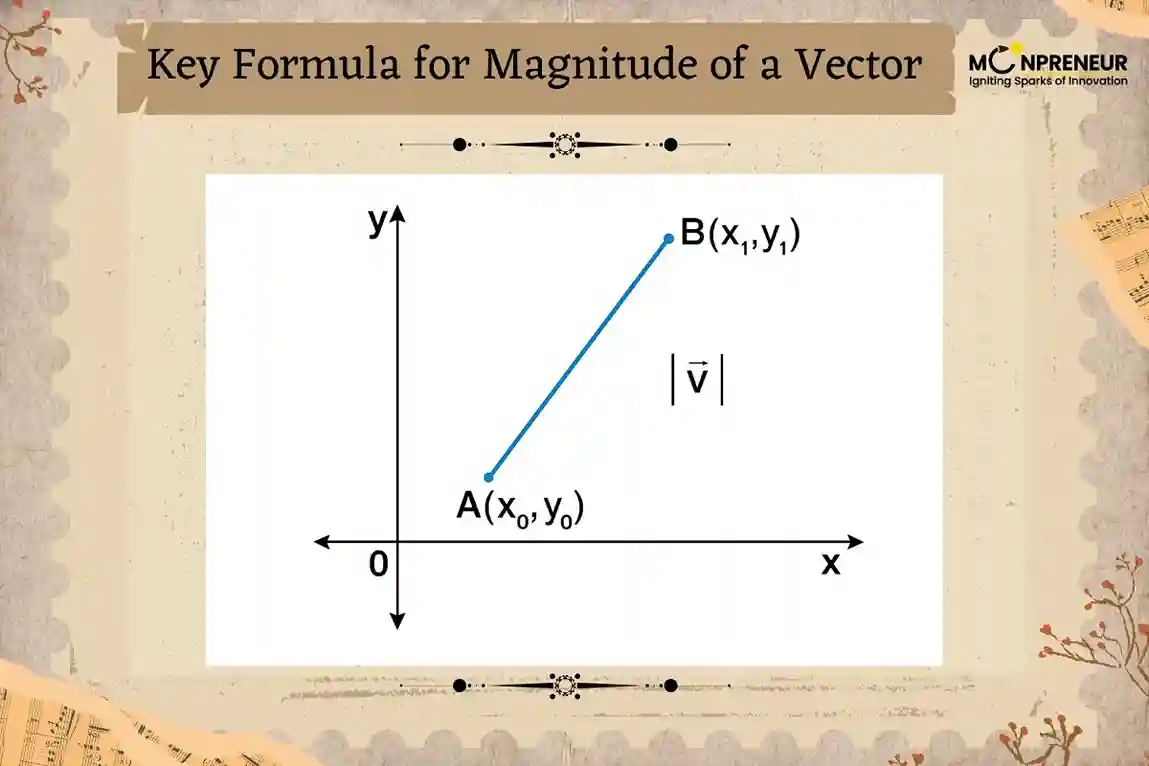
Here are the standard formulas for magnitude in 2D and 3D space:
For a vector \(\mathbf{v} = (x, y)\)
For a vector \(\mathbf{v} = (x, y, z)\)
✅ The magnitude is always a non-negative real number.
✅ These formulas are based on the Pythagorean Theorem and the distance formula.
Cross-Disciplinary Usage
- Physics → magnitude is used for velocity, displacement, and force.
- Computer Science → essential in graphics, simulations, and machine learning.
- Engineering → helps in vector mechanics and motion analysis.
- Competitive Exams (JEE, NEET, Olympiads) → vector magnitude problems appear frequently.
Step-by-Step Illustration
Let’s say we have a vector \(\mathbf{v} = (3, 4)\).
Steps to find its magnitude:
- Write down the components → (3, 4).
- Square each → \(3^{2} = 9, \quad 4^{2} = 16\).
- Add them → \(9 + 16 = 25\)
- Take the square root →\(\sqrt{25} = 5\)
So, the magnitude of vector (3,4) is 5.
Speed Trick / Vedic Shortcut
If a vector’s components match Pythagorean triples like (3,4,5) or (5,12,13), the magnitude can be found instantly.
👉 Example: For vector (5, 12), magnitude = 13 without heavy calculation.
These tricks are useful in MCQs, Olympiads, and board exams.
Try These Yourself
- Find the magnitude of the vector (6, 8).
- Calculate magnitude of (2, -3, 6).
- What is the magnitude of the vector with endpoints at (2, 3) and (7, 7)?
- Find the magnitude of (-4, -3).
Frequent Errors and Misunderstandings
Forgetting to square negative components.
Leaving out the square root step.
Confusing magnitude with direction.
Adding wrong units (magnitude is just a length, so match context: meters, newtons, etc.).
Relation to Other Concepts
- Magnitude helps in vector addition and subtraction.
- Used in dot product and cross product.
- Essential in distance calculation in coordinate geometry.
Classroom Tip
Visualize a right triangle:
- The vector’s components are the sides.
- The magnitude is the hypotenuse.
This simple mental image helps students recall the formula quickly.
Wrapping It All Up
The magnitude of a vector is the measure of its size or length, calculated using the Pythagorean theorem. It is fundamental in mathematics, physics, engineering, and competitive exams. By mastering this concept, students can easily solve problems related to force, velocity, displacement, and distance.
Keep practicing with more examples to gain confidence in vectors!
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
FAQs on Magnitude of a Vector
A: Its magnitude is 0, since all components are zero.
A: No, magnitude is always non-negative.
A: It represents the size of quantities like force, velocity, displacement, etc.
A: Magnitude = size, while direction = orientation of the vector.












