Hey there! If you’ve ever wondered about the relationship between speed, velocity, and acceleration, you’re in the right place. Whether you’re a student, a parent, or just someone curious about the science of motion, this blog will help you to understand acceleration in a simple, easy-to-follow way.
In this complete guide, we’ll cover:
What is Acceleration?
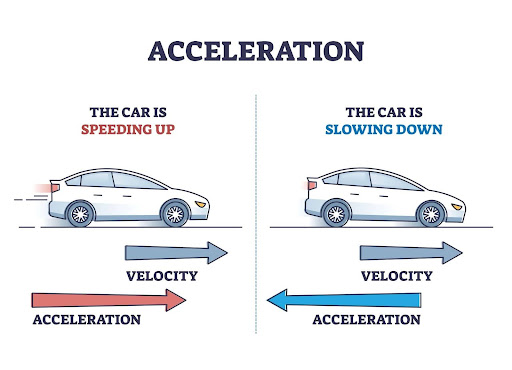
Acceleration is the rate at which an object changes its velocity. If an object speeds up, slows down, or changes direction, it experiences acceleration. Acceleration is an essential concept in physics that helps explain how things move.
Acceleration, in simpler terms, is like the feeling you get when a car speeds up or slows down. It’s the change in speed over time, and it’s happening all around us, all the time.
Units of Acceleration:
Acceleration is measured in meters per second squared (m/s²). This means that for every second, the velocity of an object increases (or decreases) by a certain number of meters per second.
Speed vs. Velocity: What’s the Difference?
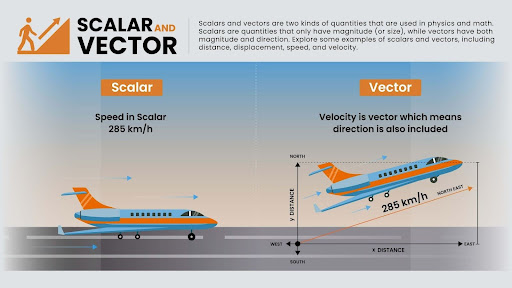
Before we delve into acceleration, it’s crucial to grasp the practical implications of understanding the difference between speed and velocity. This knowledge is not just theoretical, but it has real-world applications in various fields, from sports to engineering.
- Speed is a scalar quantity—it only tells you how fast something is moving.
- Velocity, on the other hand, is a vector quantity, which means it includes both speed and direction.
The Formula for Acceleration
To calculate acceleration, you’ll need this simple formula:
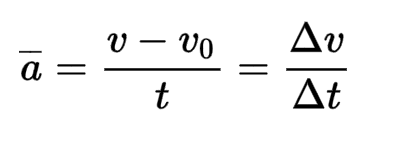
Where:
- vf is the final velocity
- v0 is the initial velocity
- t is the time taken for the change in velocity
This formula tells us that acceleration is the change in velocity over time.
Quick Tip for Remembering:
Think of acceleration as how quickly you can go from standing still (0 m/s) to running at full speed (your final velocity). The faster you achieve this, the greater your acceleration!
How to Find Acceleration with Mass and Force
The formula to find acceleration from force and mass values:
a = F/m
How to Calculate Acceleration Step-by-Step
Here’s a step-by-step example of how to calculate acceleration:
Example Problem:
A car accelerates from 0 m/s to 20 m/s in 5 seconds. What is its acceleration?
1. Identify the values:
- Initial velocity (viv_ivi): 0 m/s
- Final velocity (vfv_fvf): 20 m/sTime (ttt): 5 second
2. Conclusion: The car’s acceleration is 4 m/s².
This means the car’s velocity increases by 4 meters per second every second.
Real-Life Examples of Acceleration
- Free Fall: When an object falls due to gravity, it accelerates toward the Earth at approximately 9.8 m/s². This is a natural acceleration caused by the force of gravity.
- Driving a Car: When you press the gas pedal, your car accelerates. If you’re merging onto a highway and increase your speed from 30 km/h to 60 km/h in 10 seconds, you can calculate your car’s acceleration using the same formula!
- Roller Coasters: The thrilling feeling you get as you accelerate downhill on a roller coaster is a real-world example of high acceleration.
How To Find Average Acceleration
The formula for average acceleration (a¯) is the change in velocity, the final velocity minus the initial velocity, divided by the change in time.
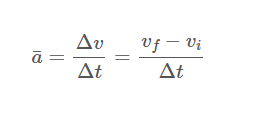
Conclusion
Now that you understand the basics of how to find acceleration and the differences between speed and velocity, you can confidently solve physics problems related to motion. Whether it’s calculating the acceleration of a car or understanding the forces behind everyday movements, mastering these concepts is crucial for anyone interested in physics.
So, the next time you see a car speed up or feel yourself being pushed back in your seat on a roller coaster, you’ll know exactly what’s happening!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Frequently Asked Questions (FAQs)
No, acceleration can be negative, which is called deceleration. This happens when an object slows down instead of speeding up.
Velocity is the speed of an object in a particular direction, while acceleration refers to how quickly that velocity changes.
Common examples include a car speeding up, a ball rolling downhill, and an object in free fall.
Yes, if an object is changing direction but maintaining the same speed (like a car going around a curve), it is still accelerating because its velocity is changing.
