Update: This article was last updated on 19th March 2025 to reflect the accuracy and up-to-date information on the page.
Adding fractions might sound tricky at first, but with a little help, it can become as easy as pie – or pizza slices! In this blog, we’ll learn how to add fractions step by step, with simple explanations, real-life examples, and fun activities to make learning enjoyable. We’ll also cover adding fractions with unlike denominators, making it easier to handle fractions with different bottom numbers. To make the process interesting, we‘ll explore adding and subtracting fractions with unlike denominators and discuss adding fractions with unlike denominators games, so it’s a fun and interactive learning process. Are you ready? Let‘s get started!
What Are Fractions?

Now, before we jump directly on how to add fractions, first you should understand what is a fraction, isn’t it? Fractions are parts of a whole. Just think of you and your friends sharing a chocolate bar: if you divide it into 4 equal pieces and you eat 1, you have 1/4 of the chocolate! Fractions are expressed as numerator (the top number) and denominator (the bottom number).
When you learn about adding fractions with unlike denominators, you need to know how to deal with various bottom numbers. Games like adding and subtracting fractions with unlike denominators or playing adding fractions with unlike denominators games can make it easier to understand the concept.
Types of Fractions
- Proper Fractions: Proper Fractions are the kind of fractions in which the numerator is lesser than the denominator (e.g., 3/4).
- Improper Fractions: In this kind of fraction, the numerator is greater than the denominator (e.g., 7/5).
- Mixed Fractions: In Mixed fractions, a fraction and a whole number is added together (e.g., 2 1/3).
Did you know the word “fraction” comes from the Latin word “fractio,” which means “to break”? It’s all about breaking a whole into parts!
Steps to Add Fractions
Let’s dive into the three simple steps to add fractions:
Step 1: Same Denominator? Add the Numerators!
When the bottom numbers are the same, you can simply add the top numbers. For instance:
Step 2: Different Denominators? Find the LCM First.
If the bottom numbers are different, determine the Least Common Multiple (LCM) to make them equal.
- Determine the LCM of 3 and 6: LCM = 6. ( How to find LCM )
- Convert fractions: But how do we do that? Let’s break this down step by step.
- Suppose you and a friend each have cakes, but the slices are of two different sizes. In order to bring them together, you first have to make the slices equal to each other.
- The LCM of 3 and 6 is 6, so we will convert the fractions. For 1/3, we multiply both the numerator and denominator by 2 to get 2/6. Now both fractions have the same denominator, 6. So, rewritten fractions are:
- Add the fractions: 2/6 + 1/6 = 3/6.
- Finally, simplify: 3/6 can be reduced to 1/2 (divide the top and bottom by 3).
Imagine fractions as pieces of cakes. The sizes of the cakes have to be equal before you add slices! must match before you combine slices!
Step 3: Simplify Your Answer
Simplify the fraction to its lowest terms by dividing the numerator and denominator by their greatest common divisor (GCD). For instance:
4/8 = 1/2
(Divide both 4 and 8 by 4).
A Rhyme To Help You Remember
♫ "When adding or subtracting, make the bottoms the same,
Adjust them with multiply or divide, it’s part of the game."
♫ "Match the top, then add or take away,
Simplify at the end, that’s the way!"
How to Add Mixed Fractions?
Now we know how to add proper and improper fractions. But adding mixed fractions has separate steps. Mixed fractions consist of whole numbers and fractions, but don’t worry – the process is equally easy:
Step 1: Convert the mixed fractions to improper fractions
Once you have a mixed fraction (for example, 1 3/4), change it to an improper fraction so it will be easy to add. Here‘s what you do–
- Multiply the whole number by the denominator (1 × 4 = 4).
- Add the numerator (4 + 3 = 7).
- Leave the denominator (7/4).
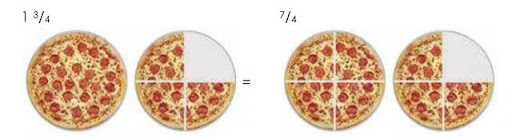
Image source: Central Bucks School District
Step 2: Add them like regular fractions
- Now, add 5/4 to the improper fraction 7/4, which we obtained by converting the mixed fraction 1 3/4.
- Add them as a regular fraction and reduce it: 7/4 + 5/4 = 12/4 = 3.
Step 3: Convert back to mixed fractions if needed
- If the solution is an improper fraction, divide the numerator by the denominator to obtain the whole number part.
- Express any remainder as a fraction to create the mixed number.
“Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding.”
– William Paul Thurston
Want to challenge yourself ? Take this Fraction Quiz
Do’s and Don’ts for Adding Fractions
| Do's | Don'ts |
|---|---|
| Find the LCM for different denominators. | Don’t forget to find the LCM. |
| Simplify the final fraction. | Don’t leave fractions unsimplified. |
| Properly separate whole numbers and fractions before adding. | Don’t mix whole numbers and fractions improperly. |
| Check your work for accuracy. | Don’t rush through the steps. |
Real-Life Applications of Adding Fractions
- Cooking: Scaling recipes (e.g., 1/2 cup + 1/4 cup = 3/4 cup).
- Sharing: Dividing candy or pizza slices.
- Budgeting: Splitting bills with friends.
Quiz Time: Practice Adding Fractions!
Q1: What is 1/4 + 2/4?
A) 3/4
B) 1/2
C) 1/4
D) 5/4
Q2: You and your friend ordered a pizza and ate 1/3 of it each. How much of the pizza did you eat together?
A) 1/3
B) 1/2
C) 2/3
D) 2/6
Q3: Simplify 7/4 + 2/4.
A) 3/2
B) 1/2
C) 9/4
D) 5/4
Q4: If you have 3/5 of a chocolate bar and your friend gives you 1/5 more, how much chocolate do you have now?
A) 4/5
B) 1/5
C) 3/5
D) 1
Q5: Convert and add 1 1/2 + 2 1/3.
A) 3 5/6
B) 3 3/4
C) 2 1/2
D) 4 1/3
Q6: You have 1/4 of a cake, and your sister has 1/3 of the same type of cake. If you combine your slices, what fraction of the cake do you have altogether?
A) 1/12
B) 1/2
C) 7/12
D) 5/12
Q7: What is the simplified form of 8/12?
A) 2/3
B) 4/6
C) 1/2
D) 8/12
Q8: What is 5/8 + 1/8?
A) 6/8
B) 1/2
C) 5/8
D) 7/8
Ans1: A) 3/4
Ans2: C) 2/3
Ans3: C) 9/4
Ans4: A) 4/5
Ans5: A) 3 5/6
Ans6: C) 7/12
Ans7: A) 2/3
Ans8: A) 6/8
Do you know?
CONCLUSION

Adding fractions doesn’t have to be hard! With these steps and regular practice, you‘ll be a fraction pro in no time. Whether you’re adding fractions with unlike denominators or problems that include adding and subtracting fractions with unlike denominators, knowing the process is essential. Practice makes perfect, so check out resources such as enjoyable adding fractions with unlike denominators games to enhance your skills and have fun at the same time. Remember, math is all about practice and understanding.
“Pure mathematics is, in its way, the poetry of logical ideas.”
– Albert Einstein
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You may choose our Advanced Math or Vedic Math+Mental Math. Our Math Quiz for 3rd, 4th, 5th, and 6th grade assists in further exciting and engaging in mathematics with hands-on lessons.














Helping my kid with fractions used to feel impossible until we tried breaking it into steps, like finding a common denominator first. Just last night, we worked on adding 3/4 and 5/6, and they nailed it! It’s such a relief to see them feeling confident with math now.
A tip I found helpful when teaching fractions is using visual aids like fraction pizzas, bars or pies. Seeing the parts visually helps kids grasp the concept of adding fractions so much faster!
This rhyme brought back memories of helping my kid with fractions! We used to make up silly songs to remember math rules, and it worked wonders. Now, I’ll teach him this one as well—it’s funny how a little rhythm can make tricky concepts stick so easily. Math is way more fun when it’s musical!