Embark on a fascinating expedition into the world of mathematics as we delve into the factors of 28. These factors are the building blocks that combine through multiplication to create the number 28. They are the linchpin of number theory, and grasping them is straightforward. Whether you’re a math enthusiast or simply polishing up your arithmetic, our guide will illuminate the unique properties of the number 28. Let’s embark on this educational journey and uncover the secrets of 28.
What Are the Factors of 28?
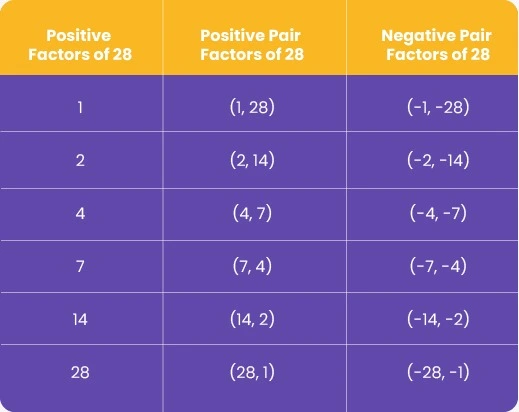
The factors of 28 are the integral numbers that, when paired and multiplied, result in 28. They are the distinct keys that fit into the lock of multiplication, revealing the number 28. The factor of 28 is unique because when you multiply 1 by 28, 2 by 14, or 4 by 7, the product is always 28. These factors come together in harmony, like a melody that resolves into a chord, to form the complete and whole number 28 with no remainders or incomplete fractions.

Pair Factors of 28
Pair factors of 28 refer to the pairs of numbers that, when multiplied, equal 28. This concept is extended to include both positive and negative pairs, reflecting the mathematical principle that the product of two negatives is a positive.
Recommended Reading: Factors of 27
Positive & Negative Pair Factors of 28:
How to Find the Factors of 28?
To determine the factors of 28, you can follow a method similar to that of finding factors of any composite number:
Initiate with 1: Divide 28 by 1. Since 28 divided by 1 is 28, both 1 and 28 are factors.
Progress methodically: Continue the process with sequential numbers. If a division by a number results in a whole number, that number is a factor of 28.
Examine for no remainder: An actual factor will divide 28 without leaving any rest behind.
Pair discovery: Once a factor is found, its complementary pair factor is the quotient of the division.
Halt at the square root: For efficiency, you only need to check numbers up to the square root of 28, approximately 5.29. Factors higher than this would have already been identified as pairs of smaller factors.
Prime Factorization of 28
The process of prime factorization breaks down a number into its prime number components. To find the prime factors of 28, one would:
Identify the smallest prime number that divides 28, which is 2.
Divide 28 by 2: 28÷2=14. So, 2 is a prime factor of 28.
Divide the quotient by the minor prime number again: 14÷2=7. So, another 2 is a prime factor.
The conclusion is that the number 7 is prime and, therefore, cannot be further divided, which establishes 7 as one of the prime factors of 28.
Therefore, the prime factorization of 28 is represented as 2 squared times 7, or 2^2 × 7, indicating that 28 is made up of two twos and a seven.
Summary
Factors of 28 take us on a mathematical quest, unveiling the numbers that, when multiplied together, form the number 28. These factors include 1, 2, 4, 7, 14, and 28 themselves. The exploration goes beyond just listing them; it shows how both positive and negative pairs, like 1 and 28 or -2 and -14, demonstrate multiplication’s inherent balance. The piece also guides readers through the process of finding these factors and breaks down the prime factorization of 28 to 2 squared times 7. This summary captures the essence of the article, offering a clear and concise understanding of the concept of factors.
Frequently Asked Questions on Factors of 27
1. What constitutes the factors of the number 28?
Factors of 28 are integers that can be multiplied in pairs to produce 28. This set includes 1, 2, 4, 7, 14, and 28.
2. How do 1 and 28 qualify as factors of the number itself?
The number 1 is a universal factor because it divides all numbers without leaving any remainder. The number itself, in this case, 28, is also a factor because it divides by itself exactly once.
3. Could you clarify the prime factorization for the number 28?
Prime factorization is the process of decomposing a number into prime numbers that multiply to result in the original number. For 28, this decomposition results in 2^2 × 7.
4. Does 28 have negative factors as well?
Indeed, for every positive factor, there is an equivalent negative one since the product of two negatives is a positive. Therefore, the negative factors are -1, -2, -4, -7, -14, and -28.
5. How are the factors of 28 utilized in everyday scenarios?
Factor knowledge is helpful in everyday scenarios such as arranging objects into groups of equal size, allocating tasks among individuals, or in fields like construction where dimensions need to be partitioned equally.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course and Math Quiz for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!













