Introduction
Arithmetic Progression (AP) is one of the most important concepts in mathematics. It represents a sequence of numbers where the difference between consecutive terms remains constant. This simple yet powerful idea is widely used in mathematics, physics, finance, and even in our daily lives.
Table of Contents

Arithmetic Progression (AP) is one of the most common types of mathematical sequences. It is defined as a sequence of numbers in which the difference between two consecutive terms remains constant.
👉 Example:
- 2, 4, 6, 8, 10 … (Common difference = 2)
- 5, 10, 15, 20 … (Common difference = 5)
This fixed difference is called the common difference (d).
We observe APs in real life too:
- Seat numbers in classrooms
- Dates in a calendar
- Even & odd numbers
- Roll numbers in a list
In an AP, the following notations are commonly used:
| Term | Representation | Formula |
|---|---|---|
| First Term | a | — |
| Common Difference | d | \(a_{2} - a_{1}\) |
| nth Term | \(a_{n}\) | \(a + (n - 1) \times d\) |
| Sum of First n Terms | \(S_{n}\) | \(\frac{n}{2} \big[2a + (n - 1)d\big]\) |
An AP can be written as: \(a, \; a + d, \; a + 2d, \; a + 3d, \; \ldots, \; a + (n-1)d\)
Here:
- a = first term
- d = common difference
- n = number of terms

The formula for the nth term is: \(a_{n} = a + (n – 1) \times d\)
Example: Find the 15th term of the AP: 3, 7, 11, 15, …
- a = 3, d = 4, n = 15
- \(a_{15} = 3 + (15 – 1) \times 4 = 3 + 56 = 59\)
So, the 15th term is 59.
The sum of the first n terms of an AP is given by:
\(S_{n} = \frac{n}{2} \big[2a + (n – 1) \times d\big]\)Example: Find the sum of the first 20 terms of the AP: 7, 10, 13, …
Solution: a = 7, d = 3, n = 20
\(S_{20} = \frac{20}{2} \big[2(7) + (20 – 1) \times 3\big] = 10[14 + 57] = 10 \times 71 = 710\)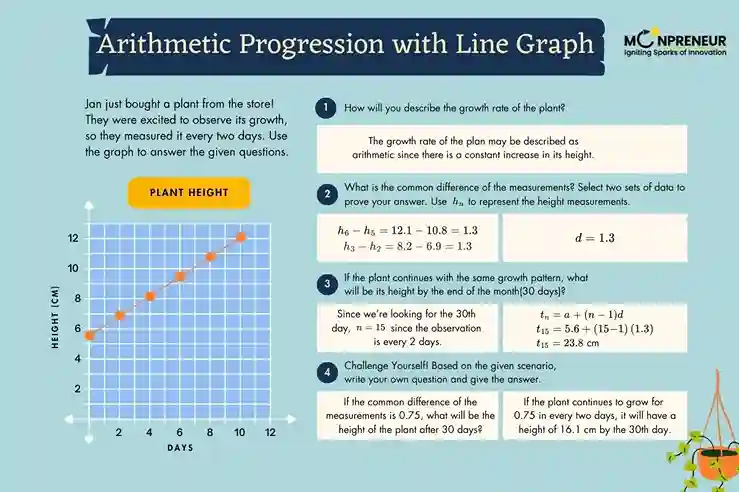
Finite AP – An AP with a limited number of terms.
Example: 5, 10, 15, 20 (ends at 20).
Infinite AP – An AP that continues endlessly.
Example: 2, 4, 6, 8, …
List of AP Formulas
Formulas of Arithmetic Progression (AP):
| Formula | Expression |
|---|---|
| nth Term | \(a_{n} = a + (n - 1)d\) |
| Sum of n terms | \(S_{n} = \frac{n}{2} \big[2a + (n - 1)d\big]\) |
| Sum when last term is known | \(S_{n} = \frac{n}{2} (a + l)\) |
Find the value of n if a = 2, d = 5, and an = 52.
- \(a_{n} = a + (n – 1) \times d\)
- \(52 = 2 + (n – 1) \times 5\)
- \(n = 11\)
Find the 15th term of the AP: 7, 11, 15, …
- \(a_{n} = 7 + (15 – 1) \times 4\)
- \(a_{n} = 7 + 56\)
- \(a_{n} = 63\)
- Find the 12th term of the AP: 5, 9, 13, …
- If a = 3, d = 7, and n = 25, find \(S_{n}\)
- Find the common difference if the 6th term is 29 and the 10th term is 45.
Conclusion
Arithmetic Progression (AP) is one of the most fundamental concepts in mathematics that builds a strong foundation for higher studies in algebra and sequences. By understanding its definition, formulas, and real-life applications, students can easily solve problems related to patterns, series, and progressions. Whether it’s calculating the nth term or finding the sum of terms, mastering AP helps sharpen logical thinking and problem-solving skills, making it a vital part of learning mathematics.
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
Step Deviation Method in Statistics – Definition, Formula, and Solved Example
What is the Frequency Formula? Definition, Examples, and Related Equations
What Is the SAT Essay? Everything You Need to Know
An overview of the SAT Math Test Sections
SAT Superscore: What It Is and Why It Matters?
Mean vs. Median vs. Mode: What is the Difference?
Mathway Reviewed: Pros, Cons, and Everything You Need to Know
Answer: \(a_{n} = a + (n – 1) \times d\)
Answer: \(S_{n} = \frac{n}{2} \big[2a + (n – 1) \times d\big]\)
Answer: Yes, if d < 0, the sequence decreases with each term.













