Update: This article was last updated on 30th September 2024 to reflect the accuracy and up-to-date information on the page.
The mystical world of mathematics—is home to confounding problems that can make even the most seasoned mathematicians scratch their heads. Yet, it’s also a realm where curiosity and intellect shine the brightest.
Here are 10 of the world’s hardest math problems, with solutions and examples for those that are solved and a humble “unsolved” tag for the puzzles that continue to confound experts.
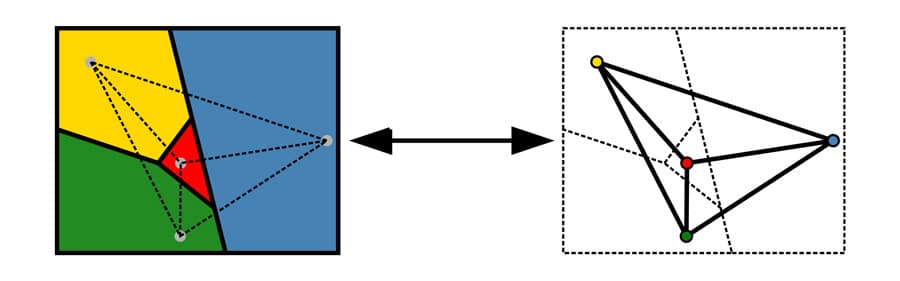
1. The Four Color Theorem
Source: Research Outreach
Problem: Can every map be colored with just four colors so that no two adjacent regions have the same color?
Status: Solved
Solution Example: The Four Color Theorem was proven with computer assistance, checking numerous configurations to show that four colors are sufficient. If you want to prove it practically, try coloring a map using only four colors; you’ll find it’s always possible without adjacent regions sharing the same color.
2. Fermat’s Last Theorem
Source: NPR
Problem: There are no three positive integers a,b,c that satisfies
an+bn=cn for n>2.
Status: Solved
Solution Example: Andrew Wiles provided a proof in 1994. To understand it, one would need a deep understanding of elliptic curves and modular forms. The proof shows that no such integers a,b,c can exist for n>2.
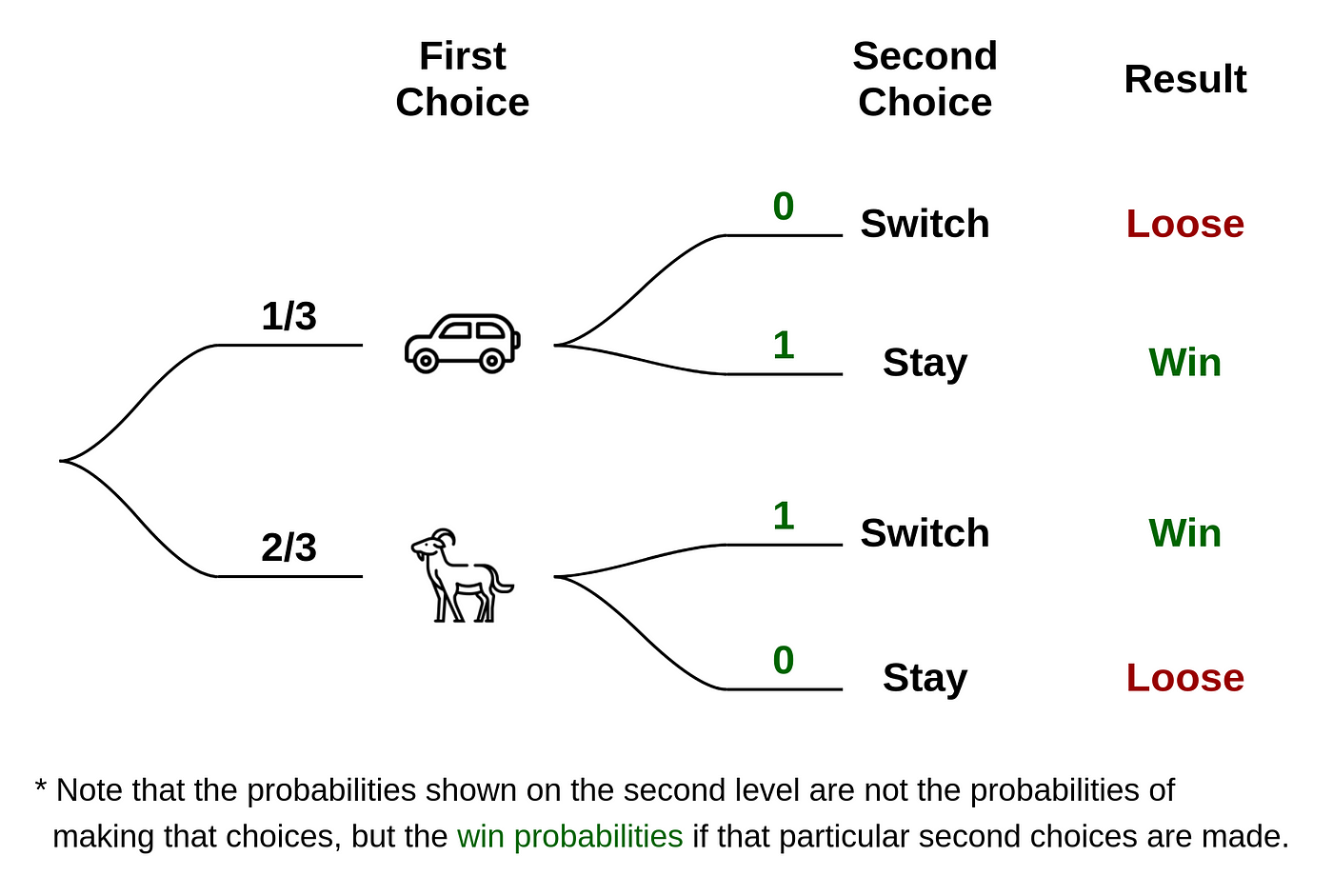
3. The Monty Hall Problem
Source: Towards Data Science
Problem: You’re on a game show with three doors. One hides a car, the others goats. After choosing a door, the host reveals a goat behind another door. Do you switch?
Status: Solved
Solution Example: Always switch. When you first choose, there’s a 1/3 chance of picking the car. After a goat is revealed, switching gives you a 2/3 chance of winning. If you don’t believe it, try simulating the game multiple times.
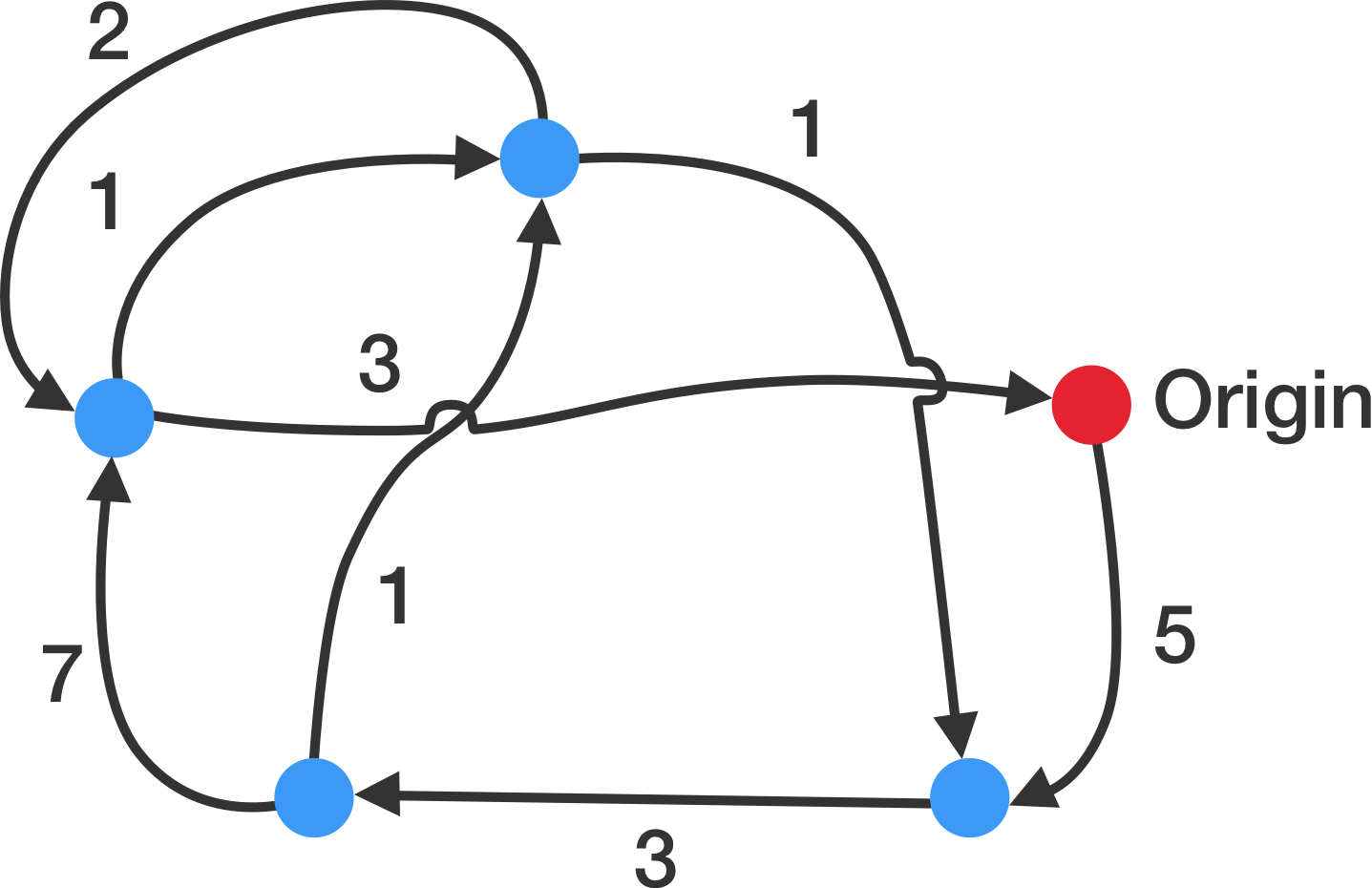
4. The Travelling Salesman Problem
Source: Brilliant
Problem: What’s the shortest possible route that visits each city exactly once and returns to the origin?
Status: Unsolved for a general algorithm
Solution Example: This is known as computer science’s most well-known optimization problems. Although there is no solution for all cases, algorithms like the Nearest Neighbor and Dynamic Programming can provide good approximations for specific instances.
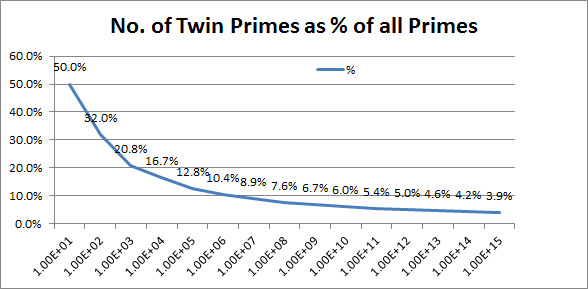
5. The Twin Prime Conjecture
Source: Hugin
Problem: Are there infinitely many prime numbers that differ by 2?
Status: Unsolved
Solution Example: N/A
Recommended Reading: Pros and Cons of Math Competition
6. The Poincaré Conjecture
Problem: Can every simply connected, closed 3-manifold be homomorphic to the 3-sphere?
Status: Solved
Solution Example: Grigori Perelman proved this using Richard Hamilton’s Ricci flow program. In simple terms, he showed that every shape meeting the problem’s criteria can be stretched and shaped into a 3-sphere.
7. The Goldbach Conjecture
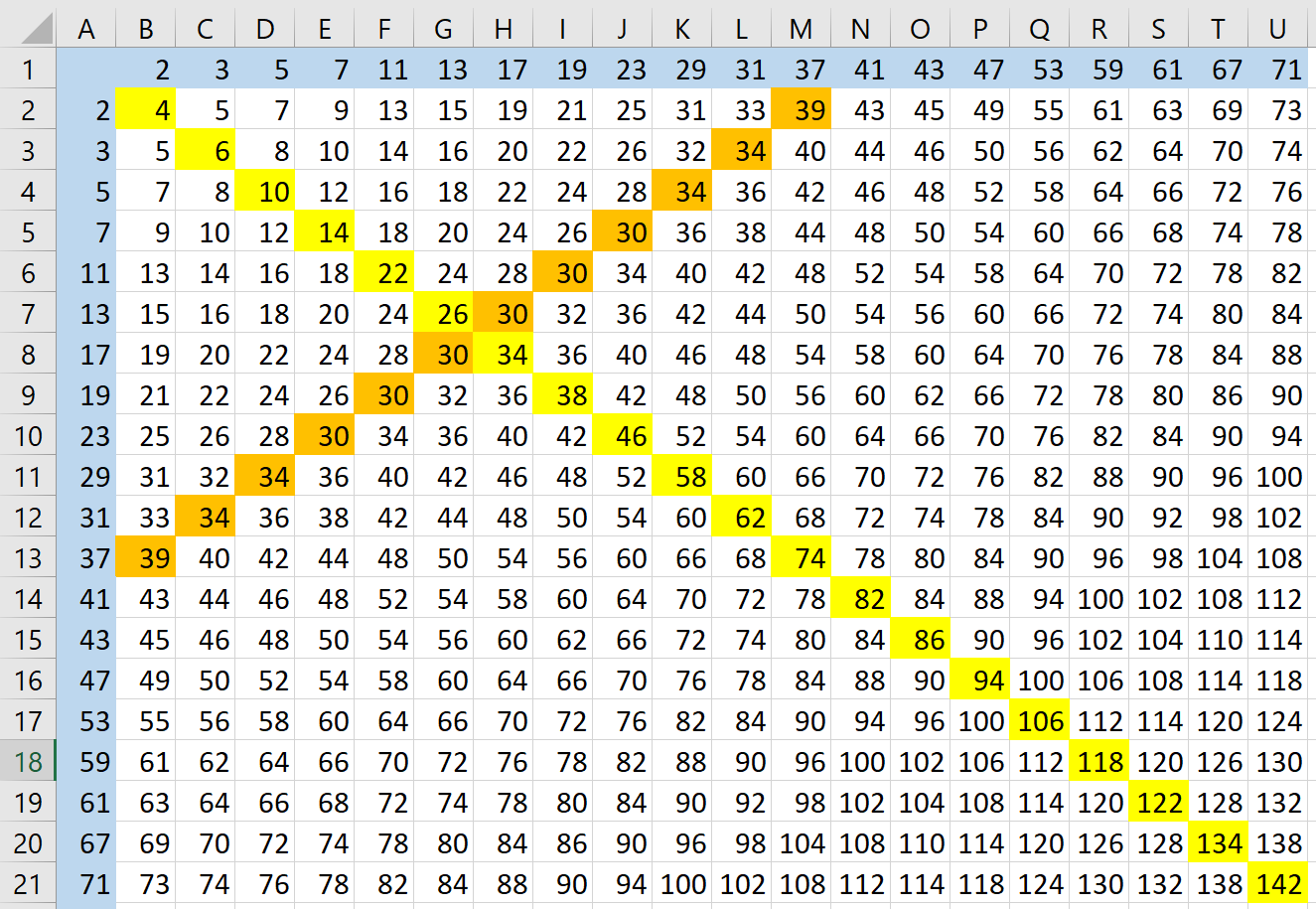
Source: Medium
Problem: Can every even integer greater than 2 be expressed as the sum of two prime numbers?
Status: Unsolved
Solution Example: N/A
8. The Riemann Hypothesis
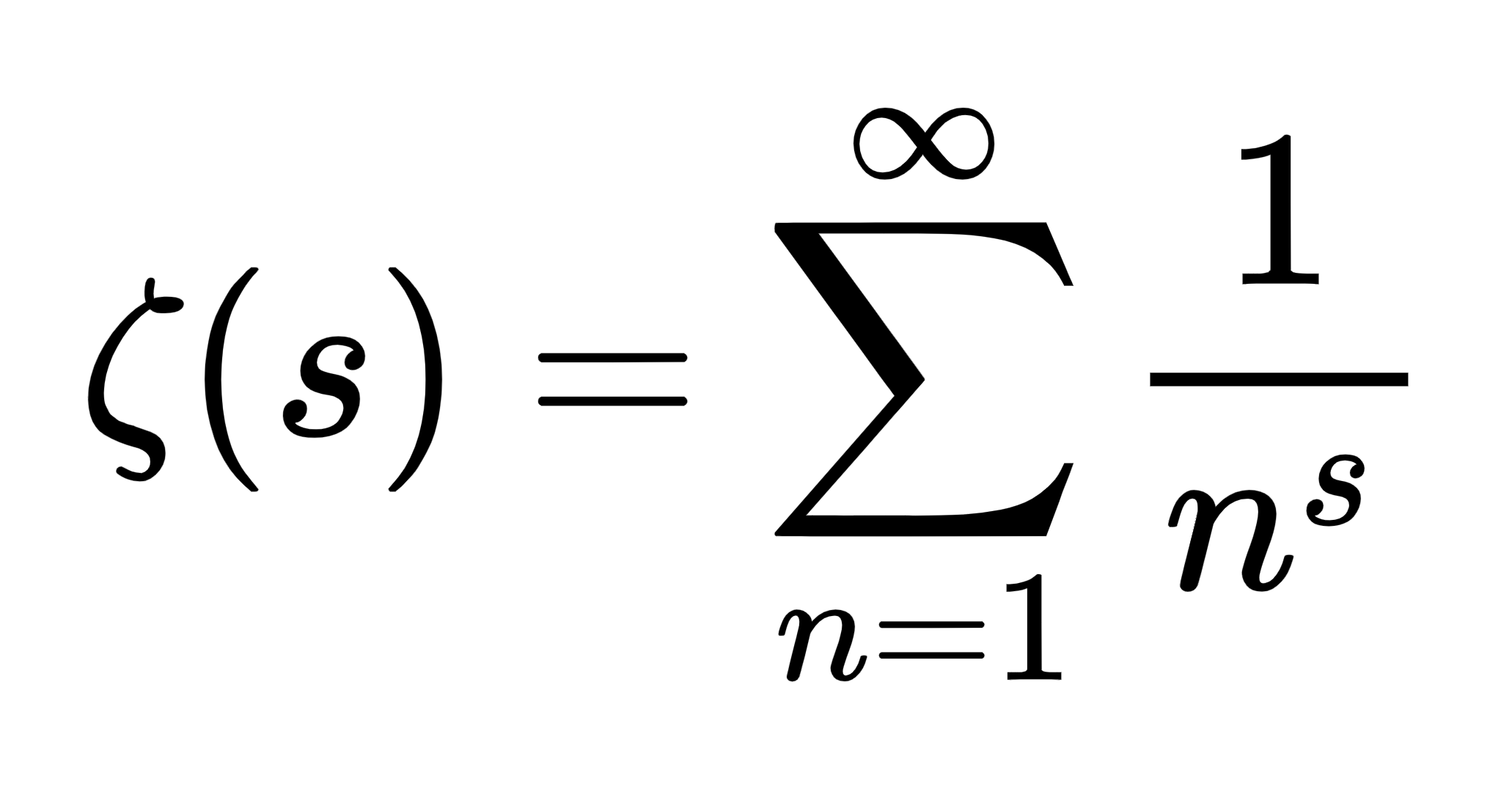
Source: The Aperiodical
Problem: Do all non-trivial zeros of the Riemann zeta function have their real parts equal to 1/2?
Status: Unsolved
Solution Example: N/A
9. The Collatz Conjecture
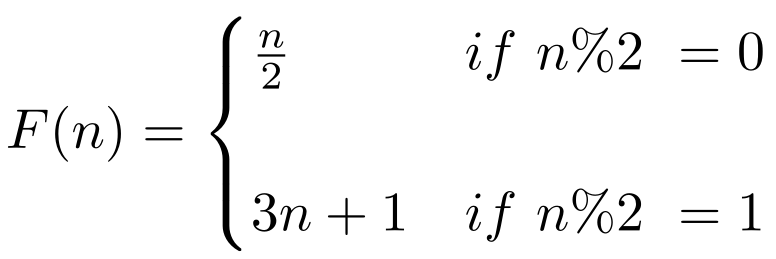
Source: Python in Plain English
Problem: Starting with any positive integer n, the sequence n,n/2,3n+1,… eventually reaches 1.
Status: Unsolved
Solution Example: N/A
10. Navier–Stokes Existence and Smoothness
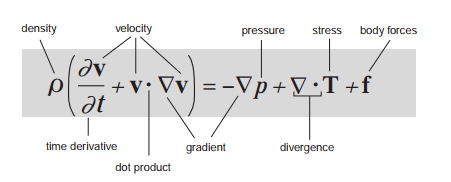
Problem: Do solutions to the Navier–Stokes equations exist, and are they smooth?
Status: Unsolved
Solution Example: N/A
The 2018 AMC stands out as the most challenging, based on statistical analysis. So let us take a look at the last two problems of AMC8 from 2018. Take a pause and try solving it yourself before you look at the solution.
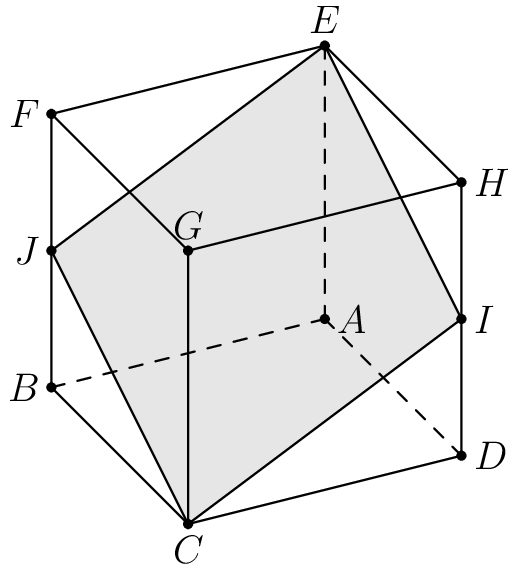
Q1. In the cube 
with opposite vertices 
and 
and 
are the midpoints of segments 
and 
respectively. Let 
be the ratio of the area of the cross-section 
to the area of one of the faces of the cube. What is 
Note that is a rhombus by symmetry. Let the side length of the cube be 
. By the Pythagorean theorem, 
and 
. Since the area of a rhombus is half the product of its diagonals, the area of the cross section is 
. This gives 
. Thus, 
.
Q2. How many perfect cubes lie between 
and 
, inclusive?
We compute 
. We’re all familiar with what 
is, namely 
, which is too small. The smallest cube greater than it is 
. is too large to calculate, but we notice that 
, which therefore will clearly be the largest cube less than . So, the required number of cubes is 
.
Conclusion
There you have it—10 of the world’s hardest math problems. Some have been gloriously solved, giving us a brilliant glimpse into the capabilities of human intellect. Others still taunt the academic world with their complexity. For math lovers, this is the playground that never gets old, the arena where they can continually hone their problem-solving skills. So, do you feel up to the challenge?
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!
FAQs
Ans- Widely accepted as the hardest and most enigmatic of all yet-to-be-solved mathematical problems, the Riemann Hypothesis was first presented in 1859 by the German mathematician Bernhard Riemann. This mathematical statement expresses an intricate pattern that lies behind prime numbers. According to this hypothesis, the location of all non-trivial zeros of the Riemann zeta function falls within a critical line in the complex plane of numbers.
Ans- A solution to the Riemann Hypothesis will have a direct impact on our understanding of the distribution of prime numbers.
It has been unsolved for over 160 years.
If it were solved, it would create a new era of Number Theory as well as modern Cryptography.
The Riemann Hypothesis is one of the Clay Mathematics Institute’s Millennium Prize Problems. A $1,000,000 reward is offered for the first correct solution.
Ans- Grigori Perelman is a mathematician who solved a math problem for $1,000,000 and then effectively vanished from view. He proved the Poincaré Conjecture in the early 2000s, which led to him receiving both the Fields Medal, awarded in 2006, and the Clay Institute Millennium Prize of $1 million, which he received in 2010. (He declined both prizes. He cited his disappointment with the mathematical community and his desire to live an isolated life and left mathematics entirely.)
Ans- Although AI has advanced greatly in assisting mathematicians in their search for new mathematical concepts, developing cutting-edge algorithms, and investigating ways to approach challenging unresolved questions; due to the inherent limitations of the current generation of AI technology in terms of both advanced logic and a sufficient volume of training data to allow for adequate problem solving, AI presently faces significant challenges related to solving the most challenging, never-before-solved Math questions.
Ans- The Four-Color Theorem states that any map can be coloured using four colours such that no two adjacent regions on the map will use the same colour. Its significance lies in the fact that it was the first proof of a very complicated mathematical theorem solved using a computer.
Ans- Fermat’s Last Theorem was an unsolvable problem for more than 350 years, and Andrew Wiles finally proved this theorem in 1994. This theorem is historically significant because it bridges two areas of modern mathematics: elliptic curves and classical number theory.
Ans- The result of the Monty Hall Problem indicates that by switching your selection after the host reveals a goat behind one of the doors, you have increased your odds of winning from 33% (1/3) to 66% (2/3) with a counterintuitive probability.
Ans- Even though there are many good approximations to the Travelling Salesman Problem, there are no fast and comprehensive solutions for all forms of the problem. As a result, the Travelling Salesman Problem remains an unsolvable issue in computer science.
Ans- Many of the most famous unsolved problems include: The Twin Prime Conjecture, Goldbach’s Conjecture, Riemann Hypothesis, Collatz Conjecture, and Navier-Stokes Existence and Smoothness.
Ans- Unsolved mathematics problems are inspirational and foster creative thinking; they advance technology; they make data more secure with stronger encryption; they push the boundaries of science before being solved.
does solving hard math questions even sharpen your brain? I mean I get exhausted and start panicking
Yes, solving tough math problems sharpens your brain by boosting critical thinking and problem-solving skills. While it may feel challenging, the process enhances cognitive abilities over time.
Don’t panic, take breaks, have some time, you’ll get better eventually, not immediately.
Do you know there is an award price of $1 Million for solving the Riemann Hypothesis….. THIS IS SOMETHING SOO SERIOUS!!!!