Introduction
Inferential statistics is a branch of statistics that allows us to make predictions, decisions, or conclusions about a population based on data collected from a sample. Instead of studying an entire population—which is often impractical—researchers use sample data to infer trends, relationships, and probabilities. This method is essential in research, business, healthcare, and various scientific fields.
Definition of Inferential Statistics
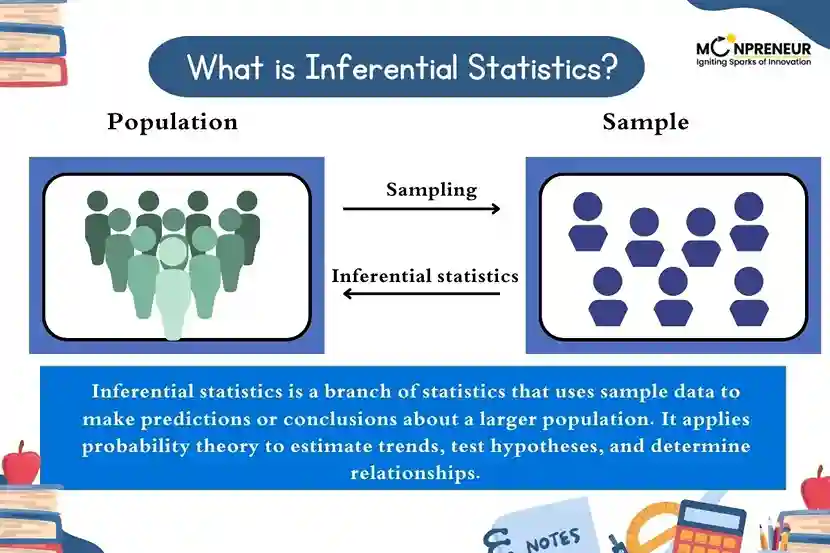
In simple terms, inferential statistics involves using sample data to estimate or test hypotheses about a population. It relies on probability theory to determine how likely it is that the conclusions drawn from the sample apply to the entire population.
Why is Inferential Statistics Important?
- Helps make decisions without testing every individual in a population.
- Saves time, money, and effort.
- Allows predictions about future trends and behaviors.
- Forms the backbone of scientific research and evidence-based decision-making.
Types of Inferential Statistics
1. Estimation
This involves using sample data to estimate population parameters such as mean, proportion, or standard deviation.
- Example: Estimating the average height of students in a school by measuring only 50 of them.
2. Hypothesis Testing
This method tests assumptions or claims about a population.
- Example: Testing whether a new teaching method improves student performance compared to a traditional method.
3. Regression Analysis
Used to determine relationships between variables and make predictions.
- Example: Predicting house prices based on size, location, and amenities.
4. Analysis of Variance (ANOVA)
Helps compare the means of three or more groups to see if they are significantly different.
- Example: Comparing exam scores of students taught with three different study techniques.
Steps in Inferential Statistics
- Define the Population & Sample – Identify the group you want to study and select a representative sample.
- Collect Data – Use surveys, experiments, or observational studies.
- Choose the Statistical Method – Select an appropriate technique like hypothesis testing or regression.
- Analyze the Data – Use statistical formulas or software.
- Draw Conclusions – Interpret the results to make decisions or predictions.
Real-Life Examples of Inferential Statistics
- Predicting election results using exit polls.
- Estimating the average customer spending in a store from a sample of receipts.
- Determining if a new drug is more effective than the current one based on clinical trial data.
Key Difference Between Descriptive and Inferential Statistics
| Feature | Descriptive Statistics | Inferential Statistics |
|---|---|---|
| Purpose | Summarizes data | Makes predictions/conclusions |
| Data Scope | Uses all collected data | Uses sample to infer about population |
| Examples | Mean, median, charts | Hypothesis testing, regression |
Conclusion
Inferential statistics is a powerful tool that helps us go beyond simple data summaries and make meaningful predictions. By analyzing sample data, we can understand large populations, test hypotheses, and make informed decisions in every field—from science to business. Mastering inferential statistics opens the door to deeper insights and smarter choices.
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle













