INTRODUCTION
The quotient is a component of division. A quotient emerges as the outcome of dividing one number by another. This outcome is invariably expressed as a fraction or decimal number.
Here are illustrative examples of quotients
4 ÷ 2 = 2
In this equation
4 is dividend
2 is divisor
2 is quotient
7 ÷ 3 = 2.333… (representing two and one-third as the quotient), and 10 ÷ 5 = 2 (with two being the quotient).
UNDERSTANDING THE QUOTIENT
Let’s elaborate further. A quotient is essentially the result obtained when one number, referred to as the dividend, is divided by another, known as the divisor. The quotient itself is the answer to this division process.
For instance, in the equation 12 ÷ 3 = 4, we identify 12 as the dividend, 3 as the divisor, and 4 as the quotient.
WHAT CONSTITUTES A QUOTIENT IN DIVISION?
Quotient represents the number of times the divisor can be evenly accommodated within the dividend. In simpler terms, it quantifies how many groups of the divisor are needed to equal the dividend.
For a practical illustration, consider dividing 10 by 2. The outcome, in this case, is 5 because 2 fits into 10 five times. Hence, 5 serves as the quotient.
Division can also be used to ascertain how many groups are present within a given number. For instance, if you divide 20 by 5, you’ll discover that there are 4 groups of 5 within 20. Consequently, the quotient is 4.
DEFINING THE QUOTIENT
In mathematics, a quotient signifies the result obtained through division, a process that involves breaking down a whole into equal parts. The quotient quantifies how many times the divisor can be accommodated within the dividend and even accounts for any remainder when the division is not perfectly even.
The term “quotient” originates from the Latin word “quotiens,” meaning “how many times.” In mathematical parlance, division by two is referred to as halving, division by three as thirds, division by four as fourths or quarters, and so forth.
The symbol for division is a slash (/). Thus, when dividing ten bananas among five children, it is expressed as 10/5 = 2. The slash between the ten and the five denotes division. This can be read as “ten divided by five equals two,” signifying that each child receives two bananas.
In cases where there are surplus bananas after each child has their fair share, we identify this as a remainder. For example, if we have eleven bananas and five children, each child receives two bananas, leaving one banana remaining.
This is represented as: 11 ÷ 5 = 2 R1, signifying “eleven divided by five equals two with a remainder of one.”
DETERMINING THE QUOTIENT: A STEP-BY-STEP APPROACH
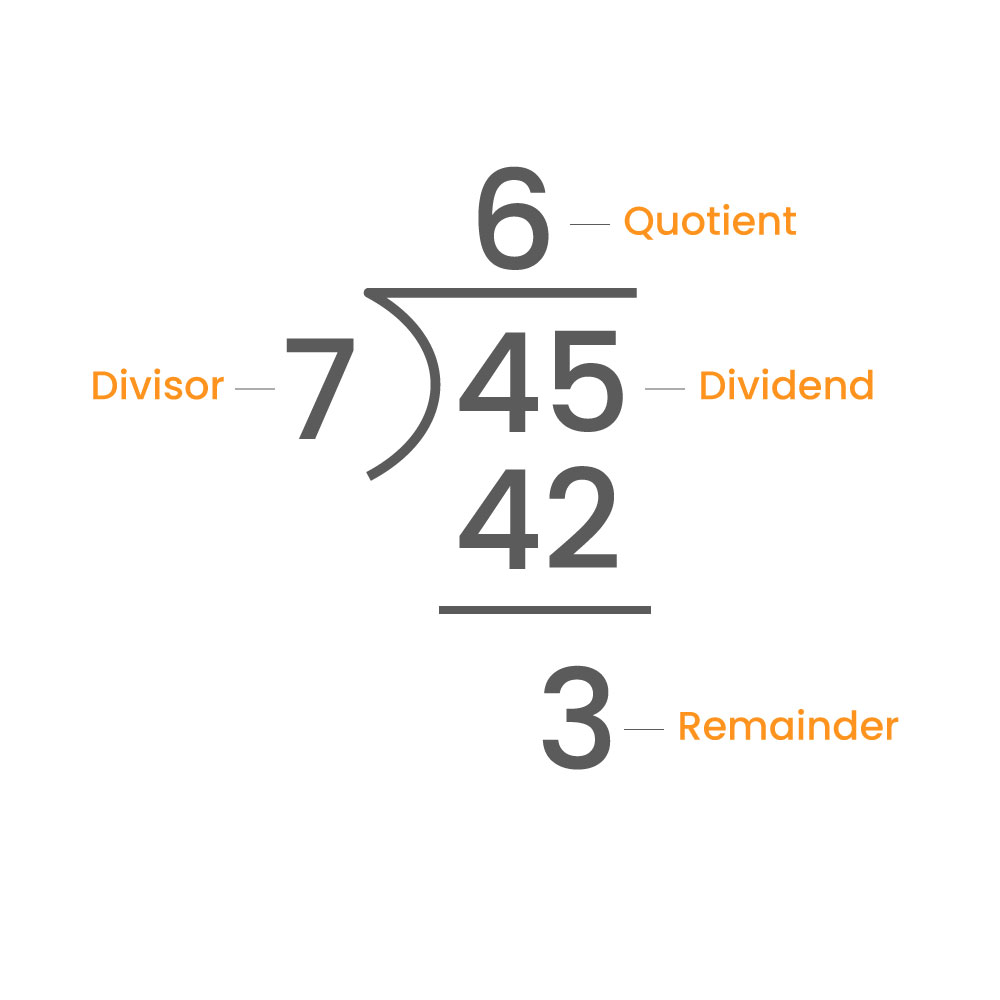
To ascertain the quotient of two numbers, the numerator should be divided by the denominator, yielding the quotient as the resultant answer.
1. Identify the Dividend: Start by recognizing the number that you want to divide. This is called the dividend. In our case, the dividend is 45.
2. Identify the Divisor: Next, determine the number by which you intend to divide the dividend. This is known as the divisor. For example: 7
3. Perform the Division: Begin dividing the dividend by the divisor. Divide the digits from left to right, one at a time, starting with the leftmost digit.
4. Record the Quotient: Write down the result of each division step as you go along. This is the quotient. In our example 6 is quotient.
5. Handle Remainders: If there is a remainder after dividing each digit, carry it over to the next digit and continue the process. Remainder is 3.
6. Check for Accuracy: Once all digits have been divided, verify the accuracy of your quotient by multiplying it by the divisor. The result should match the original dividend.
To check the accuracy follow this – Divisor x Quotient + Remainder
(6×7)+3
QUOTIENT AND REMAINDER
A quotient is the outcome of division, while the remainder signifies what remains when one number is divided by another.
For instance, dividing 10 by 3 yields a quotient of 3 and a remainder of 1.
Various methods are available for calculating the quotient and remainder. The most common approach is long division, where the dividend (the number being divided) is divided by the divisor (the number of division), with the answer displayed as the quotient, and any remaining values recorded above or to the right of it. Using the example mentioned above, a long division would appear as follows: 10 ÷ 3 = 3 R1.
Another method to determine the quotient and remainder is using a calculator, typically featuring a “÷” or “divide” button. Input the dividend first, followed by the divisor, and then execute the operation. The result will be displayed as two numbers: the quotient followed by the remainder.
In the aforementioned example, the result would be: 10 ÷ 3 = 3 with a remainder of 1.
VERIFICATION OF DIVISION RESULTS
When engaging in division, it is imperative to verify the accuracy of the division outcome. Several methods facilitate this verification process.
One method involves multiplication. To verify a division result, multiply the quotient obtained from the division problem by the divisor.
This product should match the dividend. For example, if we divide 10 by 2 and obtain a quotient of 5, multiplying 5 by 2 confirms the result. 5 times 2 equals 10, which aligns with the dividend, affirming the accuracy of the quotient.
An alternative method employs addition. To verify a division result, add all the numbers within the quotient until a single sum is achieved. This sum should match the dividend.
In the case of dividing 10 by 3 and obtaining a quotient of 3 1/3, adding 3 + 1 + 1/3 results in 10/3, which is equal to the dividend of 10. Thus, the quotient is validated.
Various other methods for verifying division results exist, but these two are among the most prevalent and straightforward. Whenever uncertainty arises regarding the accuracy of a division result, it is advisable to employ one of these verification techniques before proceeding.
PRACTICE QUESTIONS ON QUOTIENT
To reinforce your understanding of the concept, here are some practice questions related to quotients:
- What constitutes a quotient?
- How is the quotient of two numbers defined?
- What is the process for determining the quotient of two numbers?
- Can you provide examples illustrating the calculation of the quotient of two numbers?
CONCLUSION
In summary, a quotient is the result of a division operation, typically represented as a whole number. Various types of quotients are employed in mathematical equations and practical scenarios, necessitating a comprehensive understanding of their applications. We trust that this article has enhanced your comprehension of what a quotient entails and how it plays a role in everyday life.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course and Math Quiz for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!
















