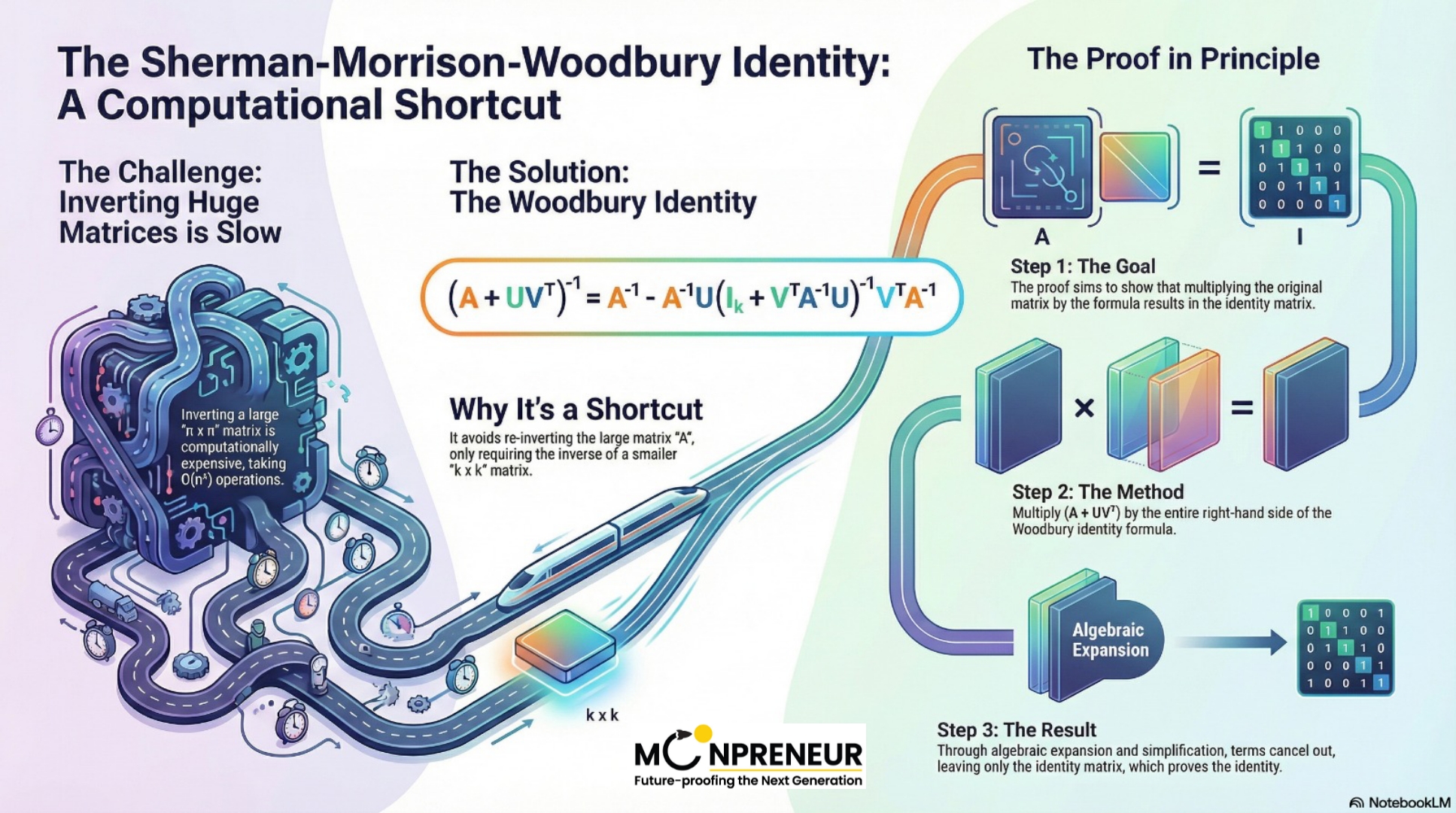
The Sherman-Morrison-Woodbury identity
\(\displaystyle (A + UV^{T})^{-1} = A^{-1} – A^{-1}U\left(I + V^{T}A^{-1}U\right)^{-1}V^{T}A^{-1}\)
Have you ever looked at a massive maths problem and thought, “There has to be a faster way”? If you’re preparing for the SATs, you’re already training your brain to spot patterns and solve equations efficiently. But what happens when the problems get even bigger—like the ones used to build Artificial Intelligence? In this blog, we are going to explore and prove the Sherman-Morrison-Woodbury identity.
Recommended Reading: How to Derive and Use the Quadratic Formula (With Examples)
The Problem: When Calculations Get Too Big
In the world of technology, we often work with “matrices”—grids of numbers. Imagine a huge matrix (A) that is 100×100 or even larger. To find the “inverse” of a matrix of that size from scratch is a massive task for a computer, requiring a huge number of operations (known as O(n³).
Now, imagine you have already solved that huge matrix, but then a little bit of new information is added to it (represented by smaller matrices U and V). If you start the whole calculation over again, you’re wasting time and energy.
For a more detailed walkthrough, you can watch this video:
The Solution: The Woodbury Shortcut
The Sherman Morrison Woodbury Identity is a way to calculate the inverse of that new, updated matrix without starting from scratch.
How it works:
If you already know the inverse of your original big matrix \(\displaystyle xA^{-1}y\)
you can use it to find the new answer by only doing “small” multiplications with the new data (U and V),
- The Logic:
Instead of one giant, slow calculation, you perform several smaller, faster ones.
- The Proof:
By multiplying both sides of the equation and simplifying the terms, you can prove that both sides are equal, showing that the shortcut is mathematically perfect.
Recommended Reading The Ultimate Guide to Solving SAT Quadratics in Seconds
Why This Matters for Your Future
You might not see 100×100 matrices on your SAT next Saturday, but this logic is the backbone of Machine Learning. When an AI learns something new, it doesn’t want to relearn everything it already knows; it uses identities like this to update its knowledge instantly.
The goal is to ensure students are preparing for the future of science and technology. Learning these concepts now helps you transition from being a student who answers questions to a scientist who builds the systems of tomorrow.
Recommended Reading: Interesting Geometry Problem to Solve For Kids
The Takeaway
Whether you are tackling an SAT algebra problem or designing an AI, always look for the “Sherman Morrison Woodbury Identity”—the logical link that lets you use what you already know to solve something new.
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.