We’ve all been there: the clock is ticking during the SAT, and you’re staring at a quadratic equation that looks like it’s going to take a full minute to factorise. When every second counts, you need more than just the “standard” way of doing things. In this blog, you are going to find the steps where you can just solve it in seconds. Yes! 2-3 seconds.
Level 1: The “Reverse the Sign” Trick
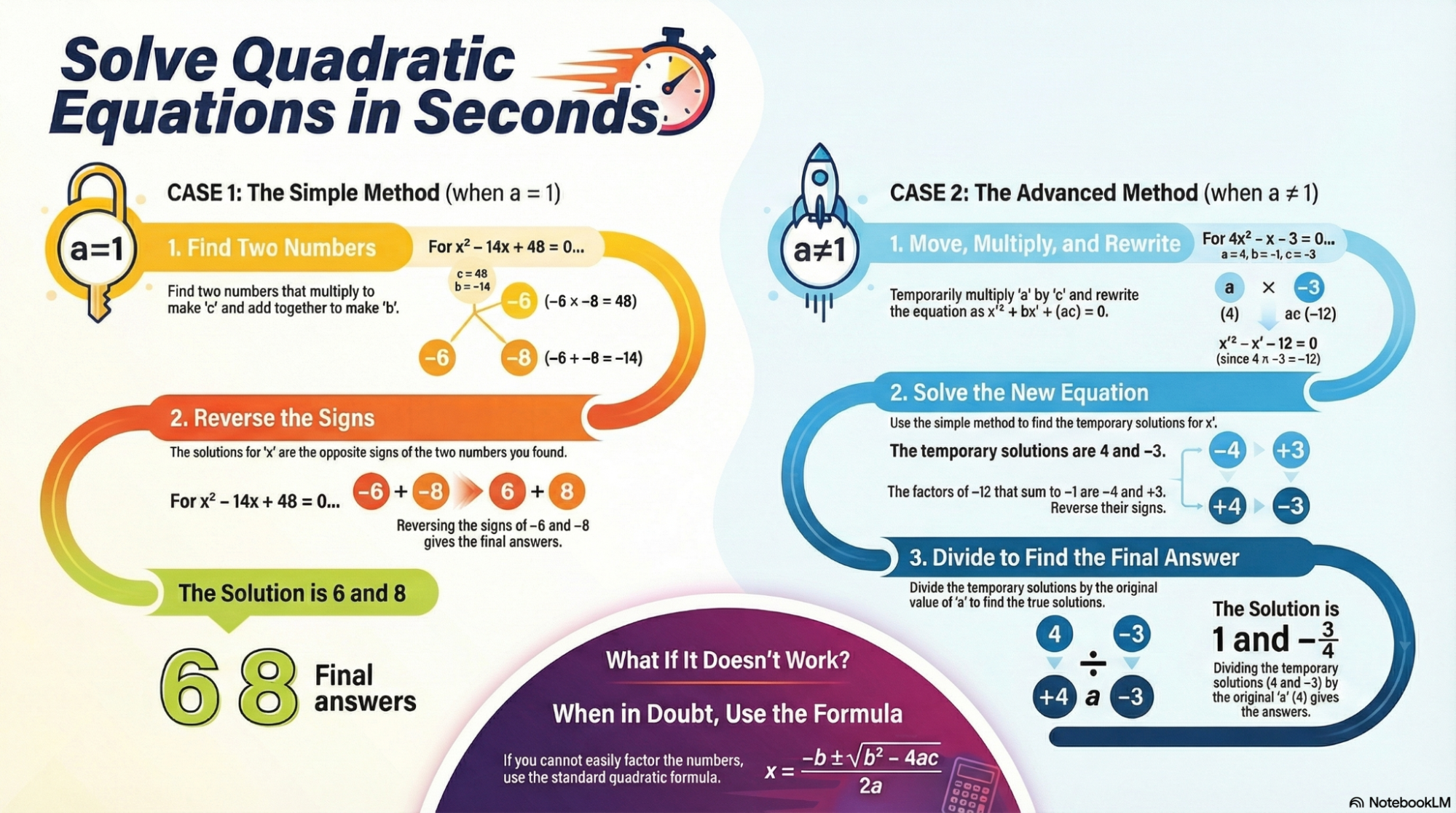
When you have a simple quadratic equation where the coefficient of x² is 1 (like x² −14x+48=0), most students start writing out multiple lines of factorisation.
The faster way:
- Find your factors: Find two numbers that multiply to the last number (48) and add up to the middle number (-14). In this case, those numbers are -6 and -8.
- Reverse the signs: Simply flip the signs of those two numbers. Your solutions are 6 and 8.
It’s that simple. Instead of writing out (x−6)(x−8)=0, you just find the factors and jump straight to the answer.
Level 2: The “Transfer and Divide” Trick
Things get tricky when x² has a coefficient greater than 1, such as 4x² −x−3=0. But we have something even better for these types of cases.
The faster way:
- Multiply a and c: Take the first number (4) and multiply it by the last number (-3). Now, imagine a new equation: x² − x − 12 = 0.
- Find the factors for the new equation: What multiplies to -12 and adds to -1? That would be -4 and +3.
- Reverse the signs: This gives you +4 and -3.
- The Final Step (Don’t forget!): Divide those numbers by the original first number (4). Your solutions are 4/4 (which is 1) and -3/4.
This method allows you to handle complex-looking problems mentally, saving you precious space on your scratch paper.
For a more detailed walkthrough, you can watch this video:
Recommended Reading: An overview of the SAT Math Test Sections
Why Does This Work?
It might feel like a “hack”, but there is real math behind it. This shortcut is actually a transformation of the quadratic formula. By shifting the coefficients, you create a temporary equation that is easier to solve, and then you “translate” the answer back to the original by dividing.
When to Use “Plan B”
As helpful as these tricks are, they rely on the equation being factorable. If you find yourself struggling to find the right factors after a few seconds, don’t panic. The sources recommend jumping straight to the quadratic formula as your reliable backup to ensure you get the right answer.
Cheat Guide to remember
- Think of the “Transfer and Divide” method like exchanging currency for a holiday.
- You multiply your money (the coefficient) to get into the local “currency” where things are easier to handle.
- You do your shopping (find your factors), but before you head home, you have to divide by that same exchange rate to see what you actually spent in your own money.
Mastering these shortcuts means you can tackle tough quadratic equations in just two or three seconds. Simply reverse your factor signs or use the transfer-and-divide method to skip the long-winded scribbling. If you get stuck, remember the quadratic formula is always there as your reliable backup plan.
Recommended Reading: How to increase your SAT Math score from 500 – 600
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.