SAT preparation has been really tough for me with lots of ups and downs and lots of learning. Let’s talk about my SAT prep experience: what I did, where I struggled and how I overcame all the obstacles that came in my way. Believe me If I could do it, then you can also do it. So, let’s start.
First of all, I was too keen on getting a good score in the SAT exam. So, I began preparing for that. I prepared hard at my own level and I was too happy at that time and felt that I am well prepared to appear for the SAT exam. Therefore, I considered taking the SAT Mock Test provided on the official website because I was quite sure that mock tests would be the deciding factor in determining where I was standing. So, I start with Math on the SAT Mock Test 4 and guess what? This test taught me a lesson which I hadn‘t anticipated.
My Mock Test 4 Experience
When I began, I realized that the questions were relatively simple and easy to manage initially but when I progressed further, the questions were becoming difficult for me to solve and at that time, I began losing my confidence. Nonetheless, I finished both modules as this would assist me in identifying my weak points where I could work upon.
Now this is the time when I went through my answers and the outcome was really shocking for me. I was able to get 530 in Module1 and 530 in Module2. Since I was anticipating a better score, I began going through the answers to know where I went wrong.
The Question I Got Wrong
Let‘s talk about the questions that I answered incorrectly from both modules and the challenges that I encountered in solving them.
From Module 1:
B) Before Hana made any monthly deposits, the amount in her bank account was $\(25\).
C) After \(1\) monthly deposit, the amount in Hana's bank account was $\(25\).
D) Hana made a total of \(25\) monthly deposits.
Explanation
Now, this question comes from the category: Linear functions. My Answer: D) but the correct answer is A). While reading this question, I didn’t give much time to understand the question and due to my negligence, I ended up selecting the wrong answer.
B) \(72^\circ\).
C) \(82^\circ\).
D) \(162^\circ\)
Explanation
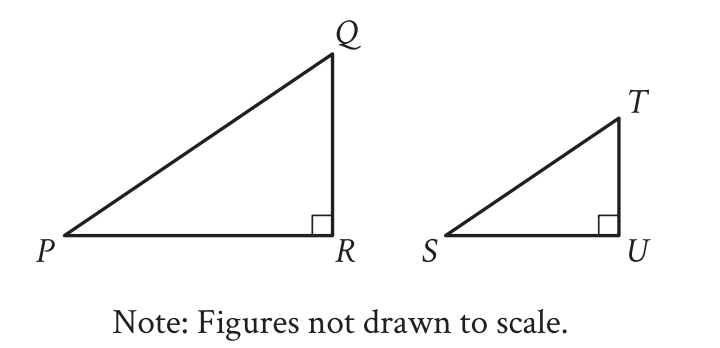
Now, this question comes from the category: Lines, angles, and triangles. My Answer: A) but the correct answer is B). While solving this question, I realized that my concepts on this topic were not strong enough which made me give the wrong answer.
B) \(y=0.9-9.4x\).
C) \(y=9.4+0.9x\).
D) \(y=9.4-0.9x\)
Explanation
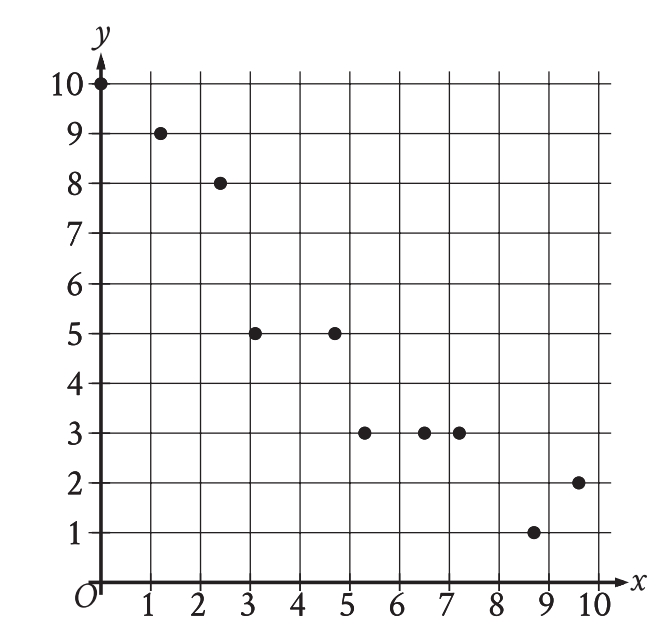
Now, this question comes from the category: Two-variable data. My Answer: A) but the correct answer is D). While solving this question, I realized that my concepts on this topic were not strong enough which made me give the wrong answer.
B) \(y=x-8\).
C) \(y=-x-8\).
D) \(y=2x-8\)
Explanation
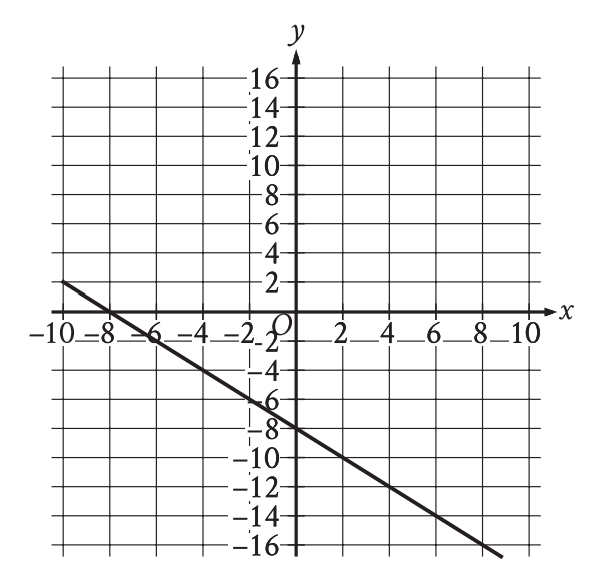
Now, this question comes from the category: Linear equations in two variables. My Answer: A) but the correct answer is C). Honestly, this question was not that hard but I didn’t pay much attention to the details and regretted it later as my concepts were clear for this question.
The given equation relates the distinct positive real numbers \(w\), \(x\), and \(y\). Which equation correctly expresses \(w\) in terms of \(x\) and \(y\) ?
B) \(w=\sqrt{\frac{ \Large 28x}{\Large 14y}}-19\).
C) \(w = \left(\frac{\Large x}{\Large y}\right)^2 - 19\).
D) \(w = \left(\frac{\Large 28x}{\Large 14y}\right)^2 - 19\).
Explanation
Now, this question comes from the category: Equivalent expressions. My Answer: A) but the correct answer is C). Honestly, this question was not that hard but I realized that I made a calculation mistake at the last step which made my whole answer incorrect.
Explanation
This question comes from the category: Circles. I didn’t attempt this question as I was completely clueless about the method of solving this question.
Explanation
Now, this question comes from the category: Equivalent expressions. This question was also not difficult to attempt but I didn’t give much time to this question because of the limited time. So, I skipped that question too.
B) \(12\).
C) \(24\sqrt{80}\).
D) \(24\).
Explanation
Now, this question comes from the category: Right triangles and trigonometry. This question was also not difficult to attempt but I didn’t give much time to this question because of the limited time. So, I skipped that question too.
B) \(-19\).
C) \(-14\).
D) \(-12\).
Explanation
Now, this question comes from the category: Linear functions. My Answer: D) but the correct answer is A). While reading this question, I didn’t give much time to understand the question and due to my negligence, I ended up selecting the wrong answer.
From Module 2:
B) \(17x^3\).
C) \(7x^3\).
D) \(17x^6\).
Explanation
Can you believe it?..Someone who is preparing for the SAT can give the wrong answer to this question? But, I did. Yes, I admit my mistake that due to my negligence and limited time, I panicked and ended up giving the wrong answer, even to this question. Unbelievable!!
B) \(15,000\).
C) \(22,500\).
D) \(45,000\).
Explanation
Now, this question comes from the category: Linear Equations in Two Variables. My Answer: D) but the correct answer is A). I found this question a little complicated to understand which made me give the wrong answer.
The function \(f\) is defined by the given equation. For what value of \(x\) does \(f(x)\) reach its minimum ?
B) \(-13\).
C) \(-\frac{\Large 23}{\Large 2}\).
D) \(-\frac{\Large 3}{\Large 2}\).
Explanation
This question was based on Calculus and I was completely aware of the concept, even I applied it too. but I realized that I made a calculation mistake at the last step which made my whole answer incorrect. My Answer: A) but the correct answer is D). You know, it feels very bad when you know how to solve the question but end up making a calculation mistake. A regretful moment for me.
B) The metal ball's minimum height was \(7\) inches above the ground.
C) The metal ball's height was \(3\) inches above the ground when it started moving.
D) The metal ball's height was \(7\) inches above the ground when it started moving.
Explanation
This question was also not difficult to attempt but I didn’t give much time to this question because of the limited time. So, I skipped that question.
B) Exactly One
C) Exactly two
D) Infinitely many
Explanation
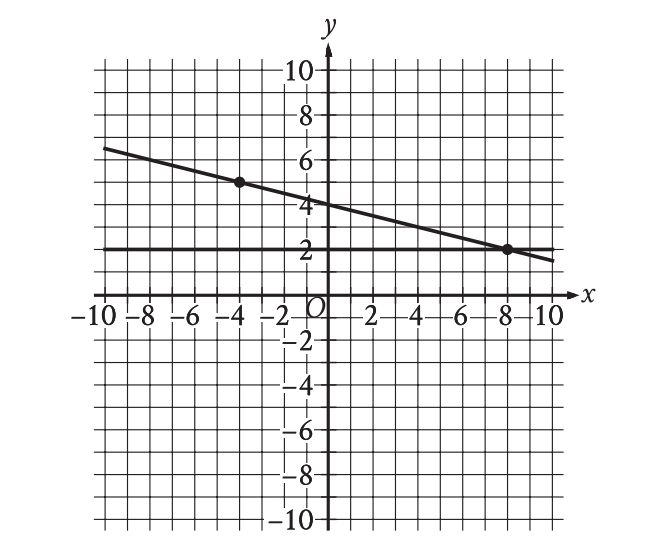
To be honest, I was not completely sure about the answer of this question, so I made a quick guess and guess what? I guessed it wrong. My Answer: B) but the correct answer is A).
The function \(f\) gives the value, in dollars, of a certain piece of equipment after \(x\) months of use. If the value of the equipment decreases each \(\underline{year}\) by \(p\%\) of its value the preceding year, what is the value of \(p\) ?
B) \(5\)
C) \(36\)
D) \(64\)
Explanation
This question was taking me time to grasp the exact concept of this question and due to limited time. So, I skipped that question.
B) \(x^2+(y-3)^2=49\).
C) \((x+2)^2+(y-1)^2=49\)
D) \(x^2+(y+1)^2=49\)
Explanation
Now while solving this question, I was pretty sure that my answer would be right as I have already practiced these types of questions earlier, but this was a time of reality check. My answer was incorrect, even I was disappointed. Probably, my concepts were still not strong at that time.
B) \(8\).
C) \(9\)
D) \(16\)
Explanation
This question was taking me time to grasp the exact concept of this question and due to limited time. So, I skipped that question.
What I Learned from My Mistakes
Honestly, these mistakes discouraged me a little while reviewing the correct answers. But, it was a reminder that confidence can sometimes lead to carelessness. I realized that overconfidence can be just as dangerous as lack of knowledge. Every detail matters, and I needed to train myself to double-check, even when I was sure I was right.
The main lesson I learned? Slow down and read carefully, especially on questions that seem straightforward at first.
Measures Taken By Me To Improve My Practice and Overall Score
After taking Mock Test 4, I made some changes in my preparation strategy. First, I started practicing similar problems on topics: Circles, Right triangles and trigonometry, Power and Indices and Algebraic Expressions, and Linear equations in two variables to have a strong grip of these concepts into my brain. As there were some questions which I might be able to crack but due to limited time, I skipped them. So, I also worked on Time Management. I began solving questions by setting the timer to ensure accuracy over speed. Now, my new motive is: slow is smooth, and smooth is fast.
Additionally, I began reviewing every question I got right and wrong after giving each mock test which helps me realize where I am improving. Sometimes, the questions you get right by guessing or rushing are the ones you need to revisit the most. This approach helped me identify my small mistakes before they became big problems on test day.
Additional Resources Which Helped Me in My SAT Prep Journey
Beyond mock tests, there were some other resources as well which played a crucial role in my SAT preparation journey and helped me improve my score. Check out these extra resources:
My Final Thoughts and Advice
Mock Test 4 was a turning point in my SAT preparation journey. The questions I got wrong were not really the hardest ones, but they were the most important for me because of the lesson they carried.
If you are a student preparing for the SAT exam, then I suggest you practice more and more questions. You can even explore multiple platforms where the Mock tests are given. If you are not sure how and where to start, then I recommend you to take this SAT Math Prep Course by Moonpreneur. Always remember the mistakes you make in mock tests aren’t failures, in fact, they are the opportunities to make you better.
This was my SAT Prep Journey. Hope you find it helpful. Remember, If I can improve myself, then you too can. Last but not the least, the final piece of advice I want to give you is: embrace the mistakes because every wrong answer tells you what you need to fix. Don’t rush. Read carefully. And remember, it’s better to stumble now than on the real test.
Mock tests are where you learn, the SAT is where you show what you’ve learned. So practice, be patient and trust the process and see the magic!! All the best for your SAT Preparation Journey!!!.
Preparing for SAT Exam? Assess Your Skills with Moonpreneur’s SAT Mock Test.














