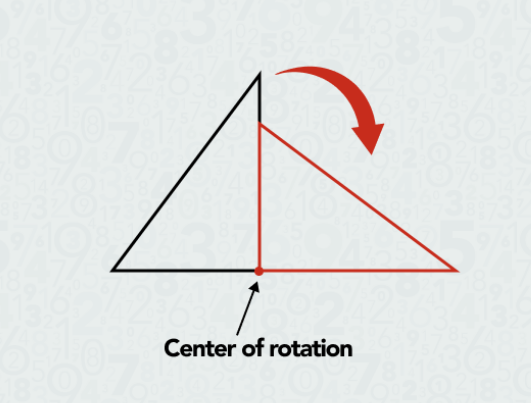
In mathematics, rotation refers to a type of transformation that turns a figure around a fixed point, known as the center of rotation. Unlike other geometric transformations like translations (sliding) or reflections (flipping), rotation involves turning the figure around a point by a certain angle. This transformation is widely used in various branches of mathematics, especially in geometry and trigonometry, and has numerous practical applications in real-world scenarios such as robotics, engineering, and computer graphics.

Key Concepts of Rotation
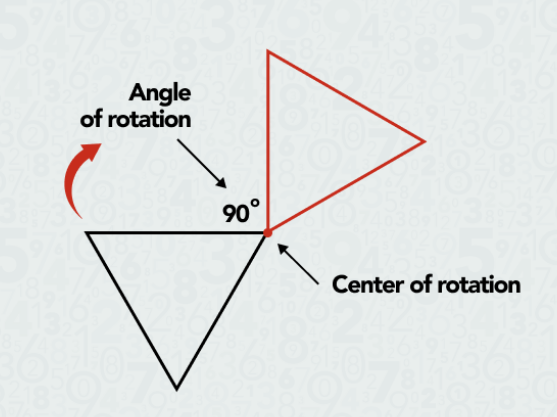
1. Center of Rotation: This is the point around which the figure rotates. It can be any point in the plane, and often, it’s the origin (0, 0) of a coordinate system for simplicity. However, it can be anywhere within or outside the figure being rotated.
2. Angle of Rotation: The angle of rotation is the measure of the degree through which a figure is rotated. This angle is typically measured in degrees (°) or radians (rad). A full rotation corresponds to 360°, while a half rotation is 180°.
3. Direction of Rotation: Rotations can occur in two directions:
- Clockwise (CW): A rotation that follows the direction of a clock’s hands.
- Counterclockwise (CCW): A rotation that goes in the opposite direction to the clock’s hands. Typically, counterclockwise is considered the positive direction in mathematics, and clockwise is negative.
4. Rotational Symmetry: Some shapes, such as circles, squares, and equilateral triangles, exhibit rotational symmetry. This means that the shape looks identical after being rotated by a certain angle, usually less than 360°. For example, a square has four-fold rotational symmetry, as it looks the same after a 90° rotation.
Rotation in Coordinate Geometry
In coordinate geometry, a rotation can be represented algebraically. Consider a point P(x,y)P(x, y)P(x,y) in the plane. To rotate this point by an angle θ\thetaθ around the origin (0, 0), the new coordinates P′(x′,y′)P'(x’, y’)P′(x′,y′) of the rotated point are given by the following formulas:
x′=xcos(θ)−ysin(θ)x’ = x \cos(\theta) – y \sin(\theta)x′=xcos(θ)−ysin(θ) y′=xsin(θ)+ycos(θ)y’ = x \sin(\theta) + y \cos(\theta)y′=xsin(θ)+ycos(θ)
This transformation can be generalized for any center of rotation by adjusting the coordinates accordingly.
Rotation Matrices
In linear algebra, rotations can also be described using matrices. A rotation matrix is a 2×2 matrix that, when multiplied by a point’s coordinates, rotates the point around the origin by a given angle. The rotation matrix for an angle θ\thetaθ is:
R(θ)=[cos(θ)−sin(θ)sin(θ)cos(θ)]R(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}R(θ)=[cos(θ)sin(θ)−sin(θ)cos(θ)]
By multiplying this matrix with a point’s coordinates, you get the new coordinates after rotation. Rotation matrices are particularly useful in computer graphics and 3D modeling.
Applications of Rotation
- Robotics and Engineering: In robotics, rotations are essential for controlling the movement of robotic arms and wheels. Understanding how an object rotates in space is crucial for designing accurate motion paths. For example, in 3D printing, rotations allow for positioning objects in various orientations during the printing process.
- Computer Graphics: Rotation is widely used in computer graphics for creating animations and rendering objects in 3D space. Game developers and animators use rotation to manipulate objects, characters, and cameras in a virtual environment, creating a sense of movement and depth.
- Astronomy: The rotation of celestial bodies, like planets and moons, is a fundamental concept in astronomy. The Earth’s rotation on its axis leads to day and night, and understanding these rotations helps in calculating time zones, eclipses, and planetary motions.
- Art and Architecture: Artists and architects use rotation in design, creating tessellation patterns and structures that are visually appealing through symmetrical rotations. For example, rotational patterns are common in Islamic art, where geometric shapes and designs are repeated with rotations.
Innovative Ideas in Rotation
One innovative approach to teaching and applying rotations is the integration of augmented reality (AR). By using AR technology, students can visualize and interact with rotating objects in real-time, helping them better understand the concept. For instance, a mobile app can allow users to rotate 3D models of geometric shapes, enabling a more immersive learning experience.
Another exciting development is the use of rotation in virtual reality (VR) for engineering simulations. Engineers can design complex systems and observe how components rotate and interact in a virtual space, providing valuable insights into mechanical systems before they are built in the real world.
Conclusion
Rotation is a fundamental concept in mathematics that transcends theoretical applications, offering practical solutions in various fields. By understanding how rotation works, from basic geometric transformations to advanced applications in robotics and computer graphics, students and professionals can better navigate the world of mathematics and its real-world applications. Whether you’re designing a new building, creating an animated character, or simply rotating a shape in a math class, the concept of rotation plays a crucial role in shaping our understanding of space and movement.
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math. You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Frequently Asked Questions
Rotation in math refers to turning a figure around a fixed point, known as the center of rotation, by a certain angle. It is a transformation that changes the position of the figure without altering its shape or size.
In coordinate geometry, rotation can be represented using formulas that calculate the new coordinates of a point after it has been rotated around the origin. The formulas involve trigonometric functions such as sine and cosine to determine the rotated point’s position.
Rotation is widely used in various fields such as robotics, computer graphics, astronomy, and engineering. For example, robots use rotation for precise movements, and rotation is key in rendering 3D models in virtual environments.
Rotational symmetry occurs when a shape looks the same after being rotated by a certain angle, less than 360°. For example, a square has four-fold rotational symmetry, meaning it looks the same after a 90° rotation.













