
Introduction:
Mathematics is like a puzzle, and each concept is a piece that fits into the bigger picture. In this blog, we will learn about one such puzzle piece i.e. the Quotient of Powers. This mathematical concept is fundamental in algebra and has applications in various fields. Let’s explore together its definition, properties, and examples, and address some common FAQs to make this topic accessible and insightful.Definition of Quotient of Powers
The quotient of powers is a mathematical expression that helps us simplify and manipulate expressions involving powers or exponents. This concept is particularly useful when dealing with variables and algebraic expressions.
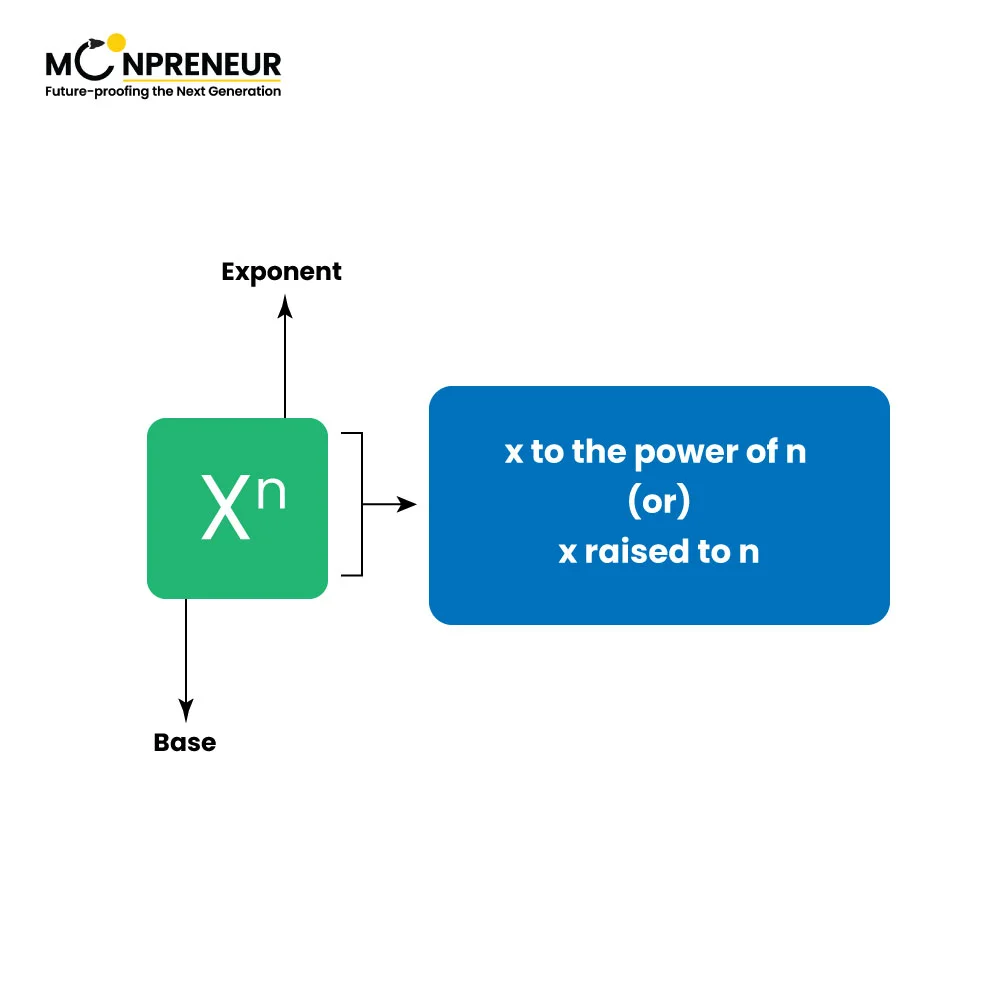
The Formula:
The formula for the quotient of powers is quite straightforward:
a^(m – n) = a^m / a^n
Here,
- ‘a’ represents the base.
- ‘m’ and ‘n’ are exponents.
Properties of Quotient of Powers:
Understanding the properties of the quotient of powers is crucial for simplifying complex expressions and solving equations. Let’s explore the key properties:
Property 1: Same Base
If you have powers with the same base (a) and you’re dividing them, you can subtract the exponents:
a^m / a^n = a^(m – n)
Property 2: Negative Exponent
When dividing with the same base, if the exponent in the denominator is greater than the exponent in the numerator, you get a fraction with a negative exponent in the result:
a^n / a^m = 1 / a^(m – n) (for n > m)
Property 3: Fractional Exponents
The quotient of powers can also be applied to fractional exponents. When dividing powers with the same base, subtract the exponents:
a^(m/n) / a^(p/q) = a^((mq – np)/(nq))
Examples:
Let’s look at some examples to illustrate how the quotient of powers works:
Example 1: Simplify the expression: (2^5) / (2^2)
Using Property 1, we subtract the exponents:
2^(5 – 2) = 2^3 = 8
Example 2: Simplify the expression: (3^4) / (3^6)
Again, using Property 1:
3^(4 – 6) = 3^(-2) = 1 / 3^2 = 1/9
Example 3: Simplify the expression: (x^3) / (x^(-2))
This time, let’s apply Property 2 and simplify:
x^3 / x^(-2) = x^(3 – (-2)) = x^5
Conclusion:
The quotient of powers allows us to simplify expressions involving exponents. Understanding its properties and how to apply them is essential for solving algebraic equations and tackling more advanced mathematical concepts. So, the next time you encounter powers or exponents in your math journey, remember the quotient of powers and simplify with confidence.













