As students, we know how intimidating high-level math can appear at first glance. Whether you are prepping for the SATs or diving into your first linear algebra course, we all share one common goal: finding a way to make complex problems feel manageable.
Today, I want to break down a legendary problem from the Putnam Linear Algebra. While Putnam is known for being incredibly tough, the logic behind this specific determinant problem is actually a fantastic lesson in pattern recognition—a skill that is gold for the SAT Math section.If you’re interested in the tech of the future, understanding how these “grids of numbers” work is your first step.
Recommended Reading: Application & Proof of the Sherman-Morrison-Woodbury Identity
The Problem: Don’t Let the Notation Scare You
The problem asks us to find the determinant of an n×n matrix A, where each entry is defined as: 1/min(i,j)
In plain English, that just means the number in each spot is 1 divided by whichever is smaller: the row number (i) or the column number (j).
Recommended Reading: How to Derive and Use the Quadratic Formula (With Examples)
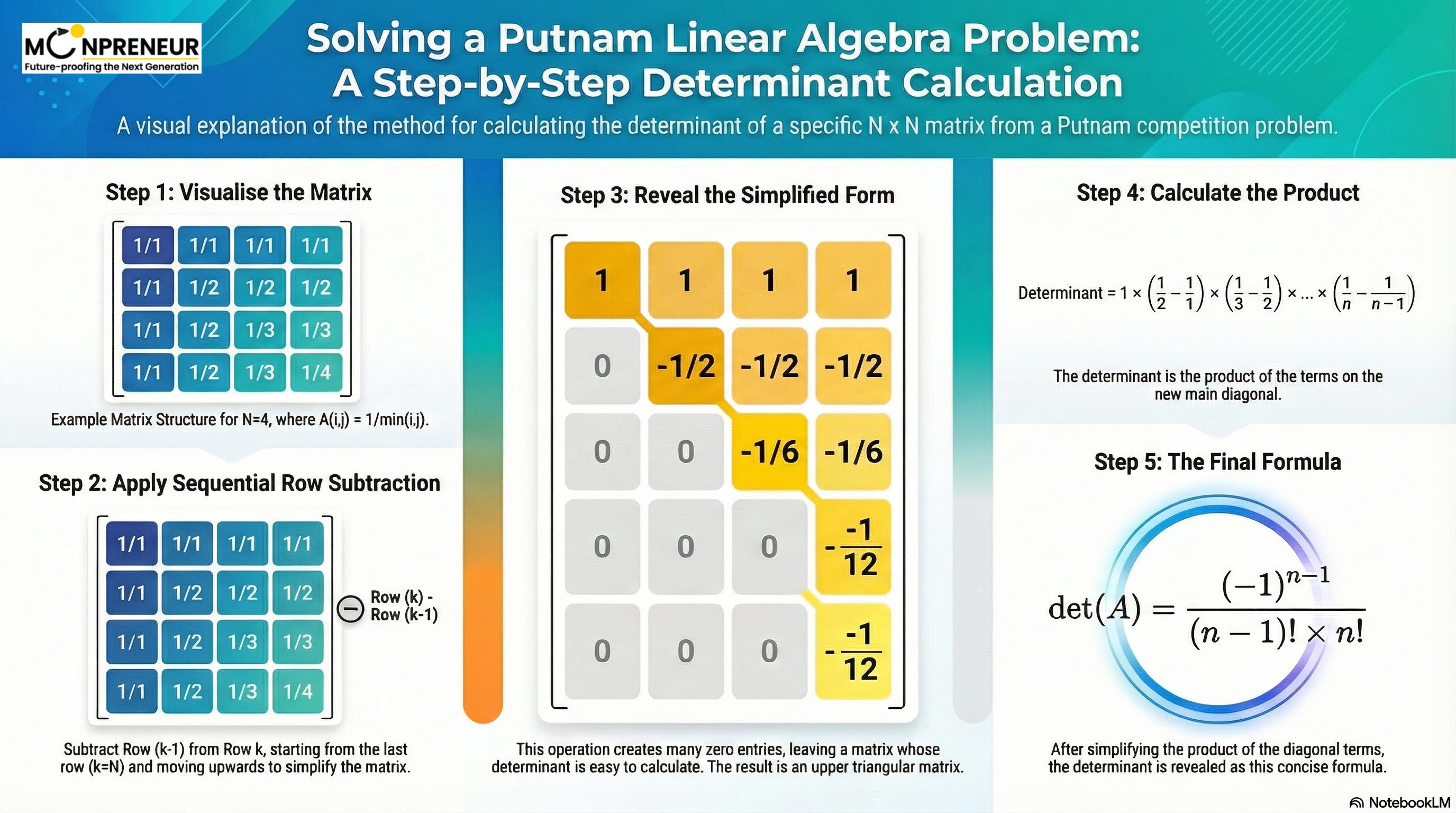
Step 1: Get a “Feel” for the Matrix
When you see a cryptic formula on a test, the best thing to do is write it out with real numbers This is a classic SAT strategy, too—if a variable expression confuses you, plug in small numbers like 1, 2, or 3.
If we write out a 5×5 version of this matrix, it looks like this:
- Row 1: 1/1, 1/1, 1/1, 1/1, 1/1 (because 1 is always the minimum).
- Row 2: 1/1, 1/2, 1/2, 1/2, 1/2 (because for the second entry onwards, 2 is the min).
- Row 3: 1/1, 1/2, 1/3, 1/3, 1/3.
- Row 5: 1/1, 1/2, 1/3, 1/4, 1/5.
Step 2: The “Zero” Trick
To find a determinant easily, you want as many zeros as possible. The secret here is row subtraction. If you subtract one row from the one below it, most of the numbers are identical and will cancel out to zero in the Putnam linear Algebra.
For example, if you subtract the 4th row from the 5th row, almost everything vanishes except for the very last term: (1/5−1/4). By progressively doing this from the bottom up, the matrix becomes much simpler, and the leading elements vanish to zero.
Recommended eading The Ultimate Guide to Solving SAT Quadratics in Seconds
Step 3: The Final Calculation
Once you’ve simplified the matrix, the determinant is just the product of those leftover diagonal terms. The pattern looks like this:
1×(1/2−1/1)×(1/3−1/2)×(1/4−1/3)⋯×(1/n−1/(n−1)).
When you do the math for each bracket, you get values like −1/2, −1/6, and so on. If you collect all the terms, the final simplified formula for the determinant is:
\(\displaystyle \frac{(-1)^{\,n-1}}{(n-1)!\times n!}\)For a more detailed walkthrough, you can watch this video:
Why Putnam Linear Algebra ?
If you’re studying for the SAT, the takeaway isn’t the formula—it’s the method:
- Don’t stop: If you don’t know the answer immediately, start writing something down to get a “feel” for the problem.
- Visualize patterns: Look for how numbers repeat or change progressively.
- Simplify: Just like we turned a big matrix into zeros, look for ways to cancel out terms in SAT algebra problems.
Recommended Reading:Interesting Geometry Problem to Solve For Kids
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.