Geometry Practice: Essential Circle and Tangent Problems for Exams

If you’ve ever looked at a geometry problem involving circles and felt like you were going in… well, circles… You aren’t alone. For many SAT students, the geometry section can feel like a collection of abstract rules, but when it comes to tangents, there are actually some very reliable “cheat codes” you can use to ace your exam.

Think of a tangent as a straight line that gives a circle a “high-five”—it touches the circumference at exactly one point and then keeps on going without ever crossing into the circle’s territory.

The “Big Three” Rules You Need to Know

To solve most SAT circle problems, you really only need to keep three major theorems in your back pocket:

1. The 90-Degree Rule: This is the most common trick on the SAT. Whenever a radius meets a tangent at the point of contact, they form a perfect 90-degree angle. If you see a tangent, immediately look for the radius. Creating that right angle often reveals a hidden right triangle, allowing you to use the Pythagorean theorem to find missing lengths.

2. The “Hat” Rule (Tangents from a Common Point): If you draw two tangents from the same external point to the same circle, those two lines are exactly the same length. It looks a bit like the circle is wearing a party hat. Because those two sides are equal, you often end up with an isosceles triangle, which is a huge clue for solving angle problems.

2. The Alternate Segment Theorem: This is for the “hard” questions. It states that the angle between a tangent and a chord is equal to the angle in the alternate segment. If you can spot this relationship, you can often find a missing angle in seconds that other students might spend minutes trying to calculate.

Your SAT Game Plan

When you encounter a complex circle diagram, don’t panic. Follow these three steps:

• Locate the key parts: Identify where the center is, where the tangents are, and where they touch (the point of tangency).
• Hunt for 90-degree angles: Draw in a radius to the point of tangency if it isn’t already there.
• Check for symmetry: If there are two tangents meeting at a point, remember they are equal in length and often form a kite shape with the radii, where the angles total 360 degrees

What is a circle?

In geometry, a circle is the collection of all the points in a plane that are at a fixed distance from a fixed point in the plane. The fixed point is called the centre, and the fixed distance is called the radius of the circle.

Key Circle Theorems & Properties

• Tangent-Radius Theorem: A tangent to a circle is perpendicular to the radius at the point of contact (90° angle).
• Two-Tangent Theorem: Tangents drawn from an external point to a circle are equal in length.
• Alternate Segment Theorem: The angle between a tangent and a chord equals the angle in the alternate segment.

Angle Properties:

• Angle at the center is twice the angle at the circumference.
• Angles in the same segment are equal.
• Angle in a semicircle is 90°.

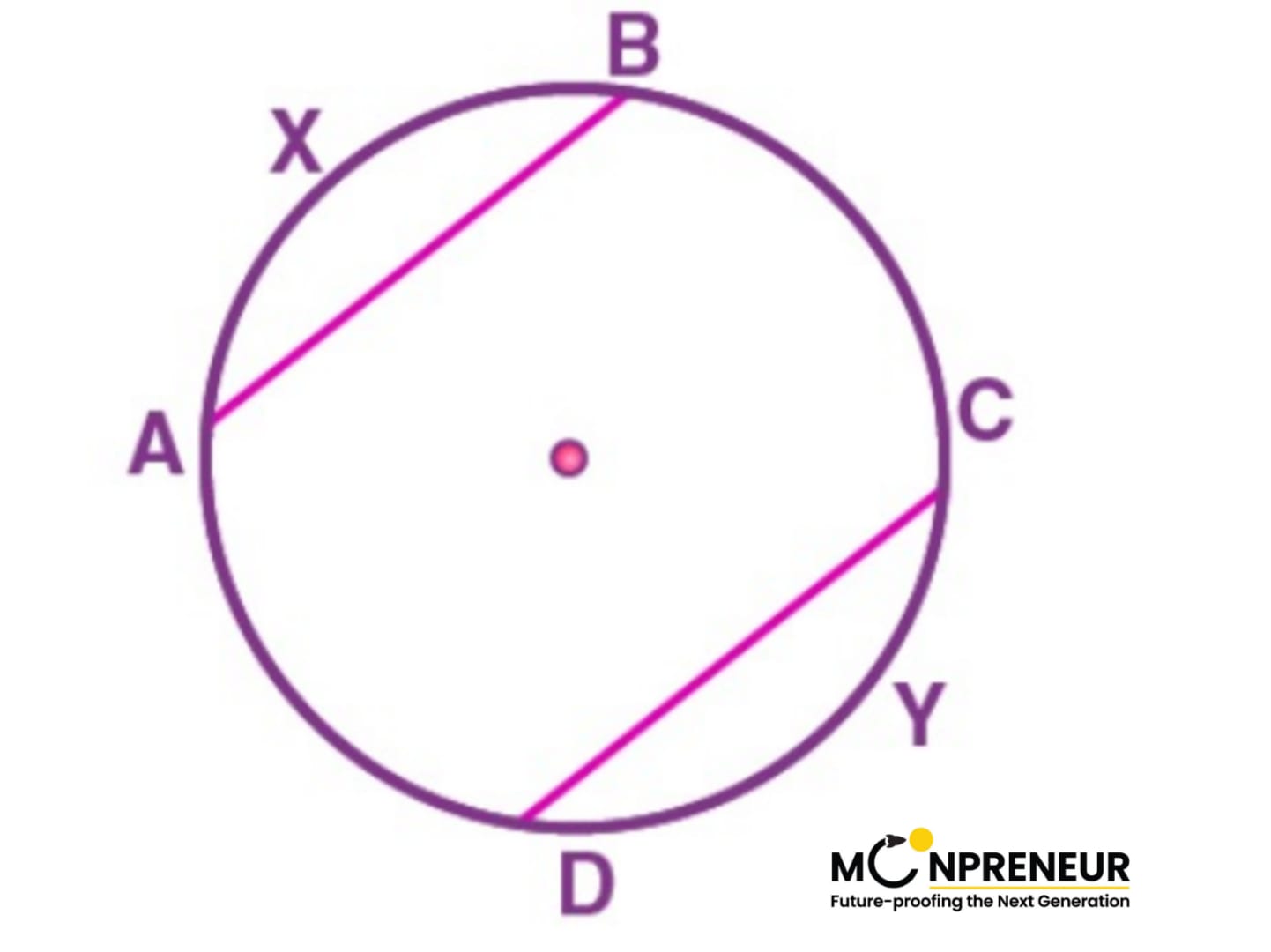
Problem 1

1. If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.

Solution:

Given that arcs AXB and CYD of a circle are congruent,

i.e. arc AXB ≅ arc CYD.

We know that if two arcs of a circle are congruent, their corresponding chords are also equal.

i.e. chord AB = chord CD

Thus, AB/CD = 1

AB/CD = 1/1

AB : CD = 1 : 1

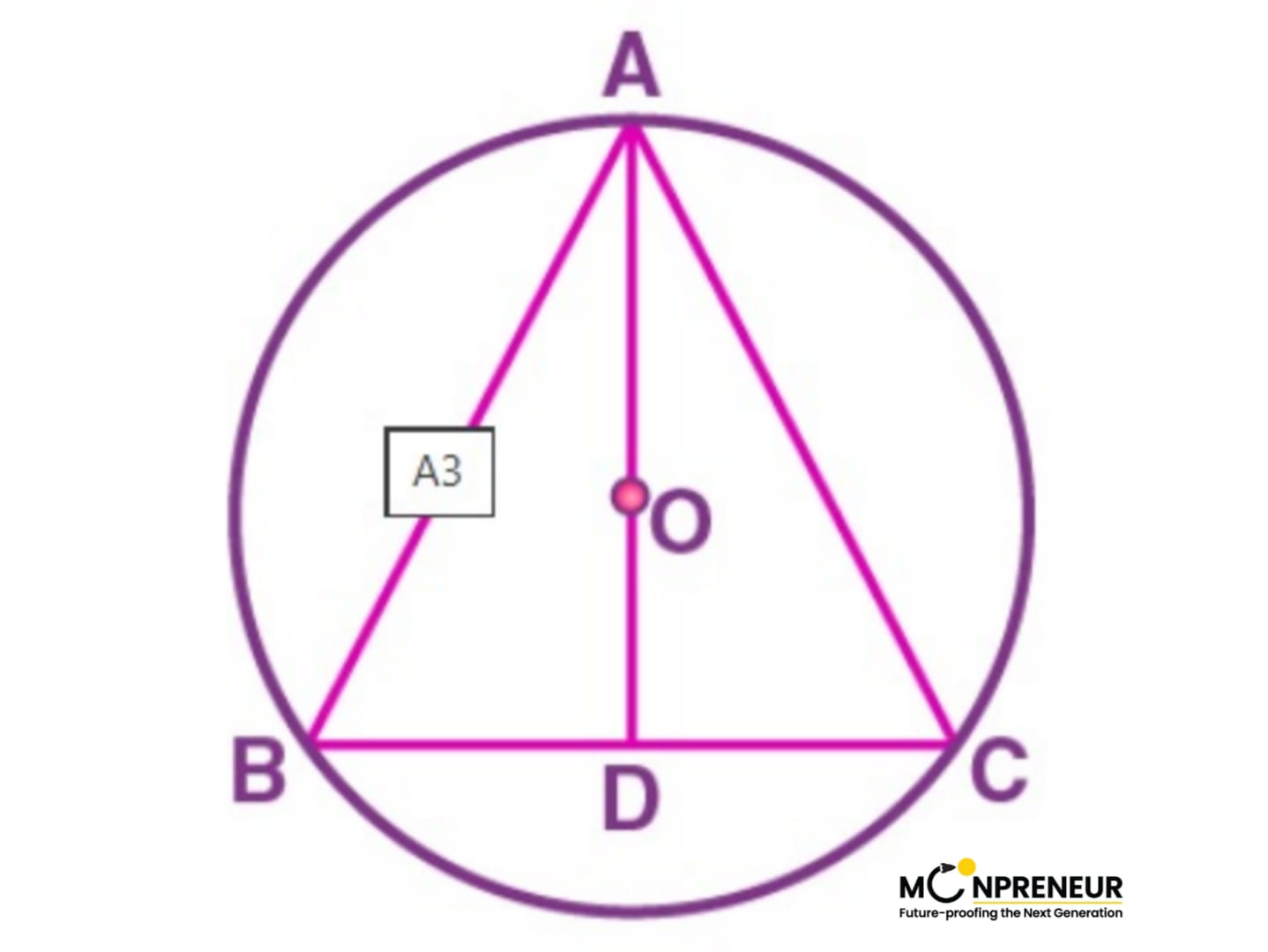
Problem 2

A circular park of a radius of 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at an equal distance on the boundary, each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.

Solution:

Let A, B, and C be the positions of Ankur, Syed and David, respectively.

As they are sitting at equal distances, the triangle is equilateral

AD ⊥ BC is drawn.

AD is the median of ΔABC, and it passes through the centre O.

O is the centroid of the ΔABC. OA is the radius of the triangle.

OA = 2/3 AD

Let a m be the side of the triangle.

So, BD = a/2 m

In ΔABD,

By Pythagoras theorem,

AB² = BD² + AD²

AD² = AB² – BD²

AD² = a² – (a/2)²

AD² = 3a²/4

AD = √3a/2

OA = 2/3 AD

20 m = (2/3) × (√3a/2)

a = 20√3 m

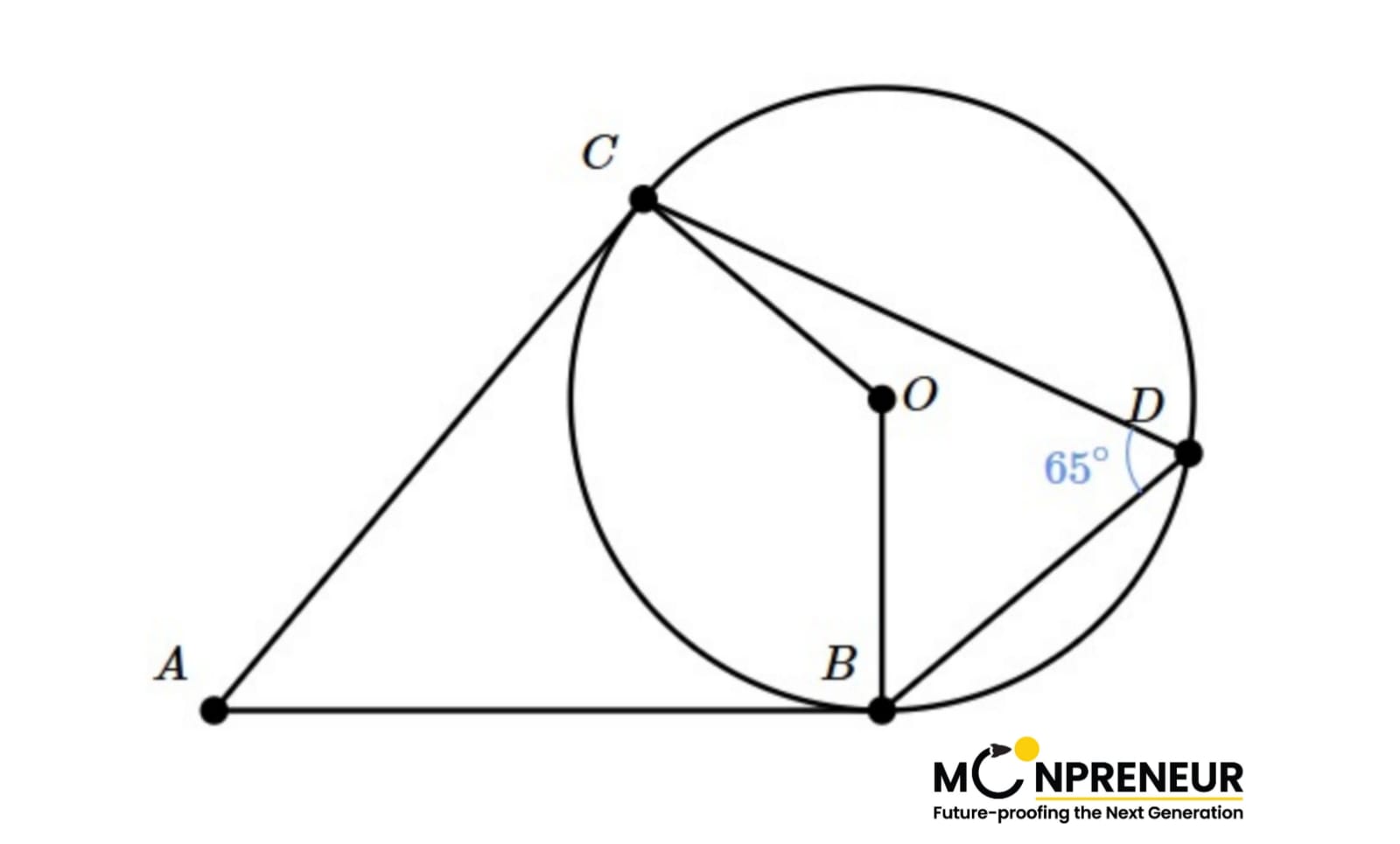
Problem 3

Angle A is circumscribed about circle O.

What is the measure of ∠A?

Solution:

1. Find the Central Angle (COB)

The Inscribed Angle Theorem states that the measure of the central angle is twice the measure of the inscribed angle that subtends the same arc.

• The inscribed angle is  ∠CDB = 65º
• Therefore, the central angle ∠COB = 2 × 65º  = 130º

2. Identify the Properties of the Tangents

The problem states that angle A is circumscribed about circle O. This means lines AC and AB are tangent to the circle at points C and B.

• A radius is always perpendicular to a tangent line at the point of tangency.
• So,  ∠ACO = 90º and ∠ABO = 90º

3. Solve the Quadrilateral ACOB

The sum of the interior angles of any quadrilateral is 360°. In the quadrilateral ACOB:

∠A + ∠ACO + ∠COB +  ∠ABO = 360º

Substitute the values we know:

∠A + 90º + 130º + 90º = 360º

∠A + 310º = 360º

∠A = 360º – 310º

∠A = 50º