As a student who has spent way too many hours staring at matrices and graphs, I know exactly how frustrating it can be when you’re prepping for the SAT and a “System of Equations” question pops up. You might be wondering: Will these lines ever meet? Why are there suddenly infinite solutions?
Lets look at Linear Equation – One Solution, No Solution, and Many Solutions
The Visual Secret: What’s Actually Happening?
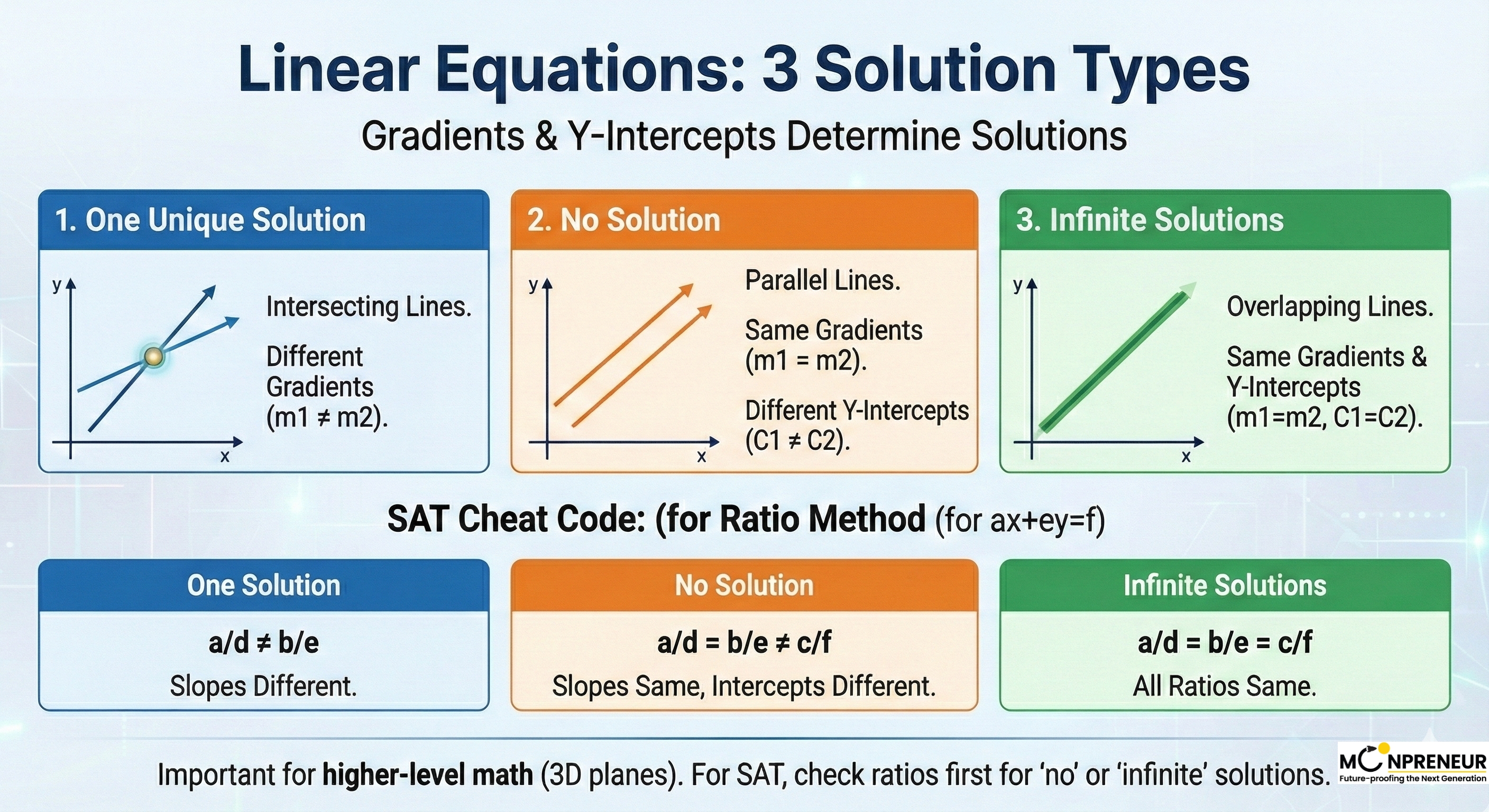
Think of two lines on a graph. According to the sources, there are only three ways these lines can behave relative to each other:
- The One-Time Meeting (One Unique Solution): This happens when the two lines have different gradients (slopes). If the gradient of the first line (m1)is different from the second (m2), they are inclined at different angles to the x-axis.
Because they aren’t parallel, they must intersect at exactly one point. If you’re solving an SAT problem and the slopes are different, you’ve got yourself a unique solution.
Recommended Reading: How to Derive and Use the Quadratic Formula (With Examples)
- The “Ghosting” Lines (No Solution): Imagine two lines running perfectly parallel, like train tracks. In this case, the gradients are identical (m1 = m2), but they start at different points on the y-axis (different intercepts, C1 =C2). Because they stay a constant distance apart, they will never intersect, meaning there is no solution to the system.
Recommended eading The Ultimate Guide to Solving SAT Quadratics in Seconds
- The Identity Crisis (Infinitely Many Solutions): Sometimes, the two equations are actually the same line in disguise! If the gradients are the same and the y-intercepts are also the same, the lines overlap completely. Every single point on one line is also on the other, giving you an infinite solution.
The SAT Cheat Code: The “Ratio Method”
When you’re under the clock during the SAT, you don’t always have time to draw a graph. The sources suggest a much faster way to check these conditions using the coefficients of the equations (when written as ax + by = c and dx + ey = f )
- One Solution: Simply check the ratio of the x and y coefficients. If a/d is not equal to e/bYou have a unique solution.
- No Solution: If \(\displaystyle \frac{a}{d} = \frac{b}{e}\) (the slopes are the same) but they do not equal the ratio of the constants c/f, the lines are parallel and will never meet.
- Infinite Solutions: If all the ratios are equal ( \(\displaystyle \frac{a}{d} = \frac{b}{e} = \frac{c}{f}\) ), the lines are identical
For a more detailed walkthrough, you can watch this video:
Why This Matters for Your Future
These same concepts of 2D lines eventually grow into 3D planes (involving x,y, and z variables) in higher-level courses like Linear Algebra or Linear Regression.
Pro Tip for SAT Students: If a question asks for “no solution” or “infinitely many solutions,” start by setting the ratios of your x and y coefficients to be equal. It’s usually the fastest way to find the missing variable.
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Recommended Readings:
- Mastering Putnam Linear Algebra: Core Concepts & Strategies
- Application & Proof of the Sherman-Morrison-Woodbury Identity
- Interesting Geometry Problem to Solve For Kids
