How to Use King’s Rule in Definite Integrals: Formulas & Solved Examples

Mastering calculus can often feel like trying to solve a puzzle with missing pieces, but every once in a while, you find a “cheat code” that makes everything click. For SAT students looking ahead to AP Calculus or those just wanting to sharpen their mathematical intuition, King’s Rule is exactly that—a powerful shortcut for solving definite integrals that look intimidating at first glance

What is King’s Rule?

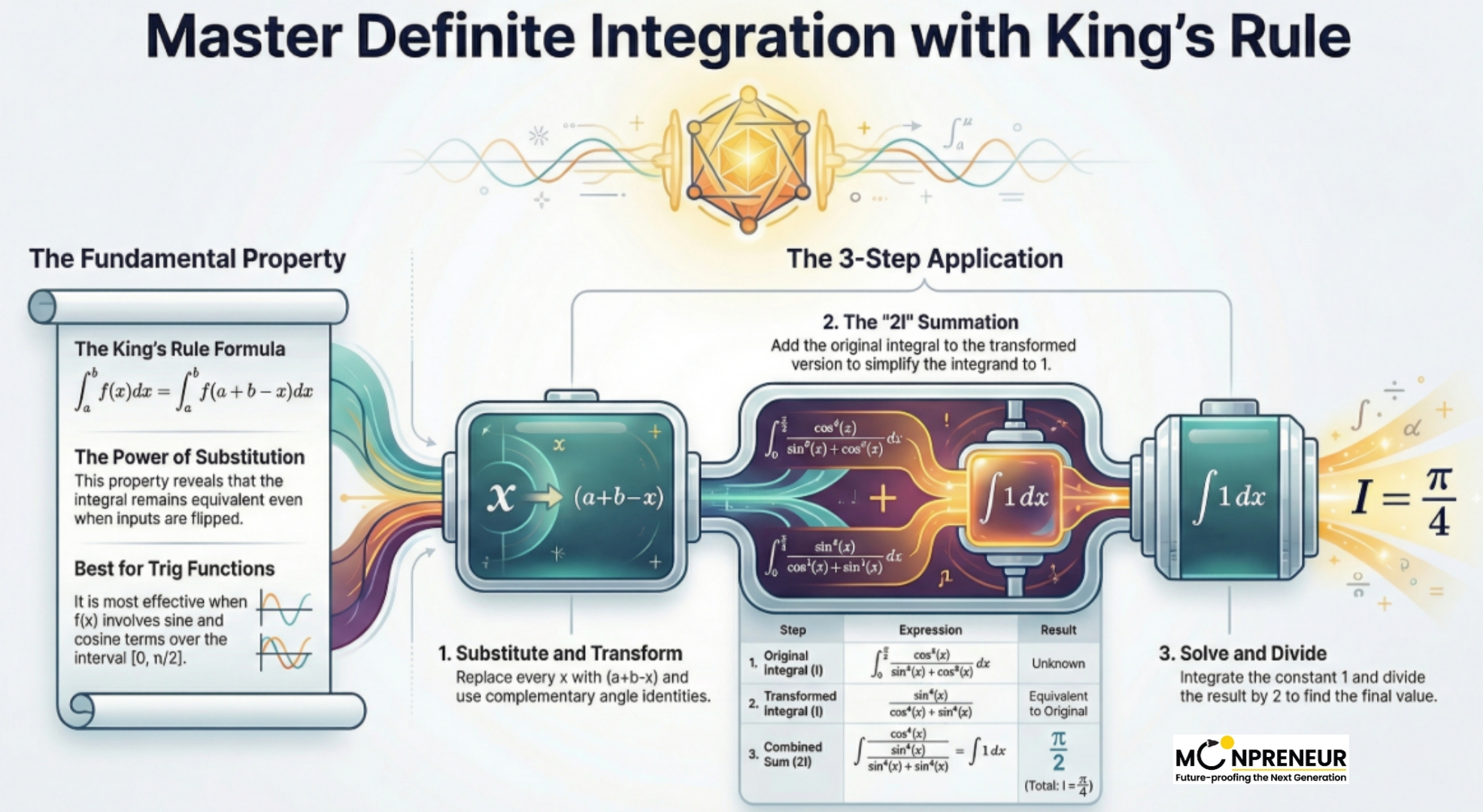
At its heart, King’s Rule is a property of definite integrals that allows you to swap the variable in a way that often simplifies the entire expression. It replaces the variable x with a+b-x (sum of limits minus x)

It states : \(\displaystyle \int_{b}^{a} f(x)\,dx = \int_{b}^{a} f(a + b – x)\,dx\)

In plain English: The area under a curve from point a to point b remains the same even if you replace every x with the sum of the limits (a+b) minus x. 

Why is it useful?

King’s Rule is typically used when:

• The integrand contains sin(x) and cos(x) (since they swap roles at π/2).
• The denominator stays the same after the substitution, allowing you to add the two integrals.
• You want to eliminate a pesky x factor (e.g., x * sin(x)).

Formula and Key Steps:

• The rule: \(\displaystyle \int_{b}^{a} f(x)\,dx = \int_{b}^{a} f(a + b – x)\,dx\)
• Step 1: Let the given integral be: \(\displaystyle I = \int_{a}^{b} f(x)\,dx\)
• Step 2: Apply the property to get \(\displaystyle I = \int_{a}^{b} f(a + b – x)\,dx\)
• Step 3: Add the two integrals: \(\displaystyle 2I = \int_{a}^{b} \bigl[f(x) + f(a + b – x)\bigr]\,dx\)
• Step 4: Simplify the integrand and evaluate.

How to Apply It: A Step-by-Step Guide

1. Identify the Bounds: Look at your limits of integration, a and b.
2. Apply the Transformation: Replace every x in your function with (a+b−x).
3. The “Double Integral” Trick: Usually, the easiest way to solve these is to call your original integral I. After applying King’s Rule, you have another version of I.
4. Add Them Together: Add the two versions (I+I=2I). Frequently, the functions will simplify into something incredibly easy, like 1, which is much simpler to integrate!

Example 1: 

\(\displaystyle \int_{0}^{\pi/2} \frac{\sin x}{\sin x + \cos x}\,dx\)

Solution:

1.Let \(\displaystyle I = \int_{0}^{\pi/2} \frac{\sin x}{\sin x + \cos x}\,dx\)

2. using King’s Rule (a= 0, b = Π/2), replace x with ( 0 + Π/2 – x): 

3. Add the two I expressions: \(\displaystyle
2I = \int_{0}^{\pi/2} \frac{\sin x + \cos x}{\sin x + \cos x}\,dx
= \int_{0}^{\pi/2} 1\,dx
\)

4.\(\displaystyle 2I = \left[ x \right]_{0}^{\pi/2} = \frac{\pi}{2}\)

5. Therefore, \(\displaystyle I = \frac{\pi}{4}\)

Example 2:

\(\displaystyle \int_{0}^{\pi/2} \log(\sin x)\,dx\)

Solution:

1. Let \(\displaystyle
I = \int_{0}^{\pi/2} \log\!\left(\sin\!\left(\frac{\pi}{2} – x\right)\right)\,dx
= \int_{0}^{\pi/2} \log(\cos x)\,dx
\)

2. Apply King’s Rule: \(\displaystyle
I = \int_{0}^{\pi/2} \log(\sin x)\,dx
= \int_{0}^{\pi/2} \log(\cos x)\,dx
\)

3. Add the Equations: \(\displaystyle
2I = \int_{0}^{\pi/2} \bigl(\log(\sin x) + \log(\cos x)\bigr)\,dx
= \int_{0}^{\pi/2} \log(\sin x \cos x)\,dx
\)

4. Using log properties: \(\displaystyle
2I = \int_{0}^{\pi/2} \log\!\left(\frac{\sin 2x}{2}\right)\,dx
\)

5. Hence: \(\displaystyle I = -\frac{\pi}{2}\log 2\)

For a more detailed walkthrough, you can watch this video: