How to Subtract Fractions
Fractions are a fundamental aspect of mathematics, and knowing how to subtract them is important in solving many real-life problems. Whether working with fractions that have the same denominator, different denominators, or mixed numbers, knowing this skill will make your math foundation stronger.
Introduction to Fractions
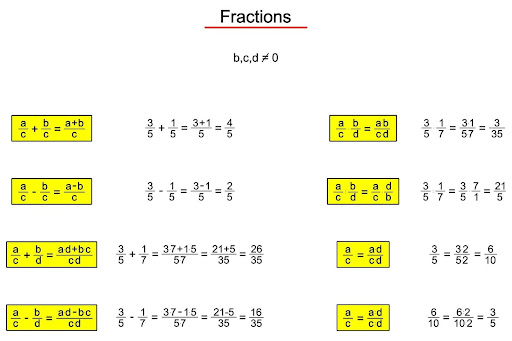
Fractions are an elementary notion in mathematics and signify a portion of a whole. A fraction is made up of two numbers: a numerator (upper number) and a denominator (lower number). The denominator indicates how much the whole is separated into equal parts, and the numerator indicates how many of these parts we possess. For instance, in 3/5, 3 signifies three parts out of 5.
Fractions are divided into various types:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 2/7, 5/9).
- Improper Fractions: The numerator is larger than or equal to the denominator (e.g., 9/4, 7/3).
- Mixed Fractions: A whole number combined with a fraction (e.g., 3 1/2, 5 2/3).
Fractions need to be understood to carry out operations such as addition, subtraction, multiplication, and division.
What is Meant by Subtracting Fractions?
Subtracting fractions involves determining the difference between two fractional values. Unlike whole numbers, fractions have special rules when subtracting them, depending on whether they share the same denominator or not.
When subtracting fractions, we do the following:
- Same Denominator: Subtract the numerators and leave the denominator as it is.
- Different Denominators: Convert the fractions to a common denominator first before subtracting.
- Mixed Fractions: Convert mixed numbers to improper fractions before subtracting.
- Whole Numbers and Fractions: Convert whole numbers into fractions for purposes of subtraction.
For example, 5/8 – 1/4 requires converting 1/4 to 2/8, making the equation 5/8 – 2/8 = 3/8. Mastering fraction subtraction is essential for solving real-world problems in measurements, finance, and science.
Recommendation Reading:
- How to increase your SAT Math score from 500 – 600
- An overview of the SAT Math Test Sections
- SAT Costs: Fees, Fee Waivers, and What to Expect
- Exponent Rules: Master the Laws of Exponents Easily
Subtraction of Fractions with Like Denominators
If fractions possess the same denominator, then they can be easily subtracted. You simply subtract the numerators while retaining the same denominator.
Steps to subtract fractions with the same denominators:
- Make certain that both the fractions share a common denominator.
- Subtract numerators.
- Take the difference on top of the common denominator.
- Simplify the fraction if attainable.
Example:
712−312\frac{7}{12} – \frac{3}{12}127−123
= 7−312=412=13\frac{7-3}{12} = \frac{4}{12} = \frac{1}{3}127−3=124=31 (simplified).
This is an easy and efficient method since both fractions are parts of the same whole. It is widely applied in cases such as subtracting slices of a pizza, measuring ingredients, or determining time differences.
Subtracting Fractions with Unlike Denominators
When fractions have unlike denominators, they need to be expressed in terms of a common denominator for subtraction. The least common denominator (LCD) is the smallest multiple shared by both denominators.
Steps:
- Determine the LCD of both denominators.
- Convert each of the fractions to have the LCD.
- Subtract the numerators and retain the denominator.
- Simplify the outcome.
For example,
56−14\frac{5}{6} – \frac{1}{4}65−41
- The LCD of 6 and 4 is 12.
- Convert fractions: 56=1012\frac{5}{6} = \frac{10}{12}65=1210, 14=312\frac{1}{4} = \frac{3}{12}41=123.
- Subtract: 1012−312=712\frac{10}{12} – \frac{3}{12} = \frac{7}{12}1210−123=127.
This is an accurate way to handle various fractions when dealing with real-life situations.
Subtracting Mixed Fractions

A mixed fraction is a whole number added to a fraction. To subtract mixed fractions, we first change them into improper fractions and then subtract.
Steps:
- Change mixed numbers to improper fractions.
- Determine least common denominator if necessary.
- Subtract the fractions.
- Convert to mixed numbers if necessary.
Example:
425−2134 \frac{2}{5} – 2 \frac{1}{3}452−231
- Convert to improper fractions:
- 425=2254 \frac{2}{5} = \frac{22}{5}452=522
- 213=732 \frac{1}{3} = \frac{7}{3}231=37
- LCD of 5 and 3 is 15.
- 225=6615\frac{22}{5} = \frac{66}{15}522=1566, 73=3515\frac{7}{3} = \frac{35}{15}37=1535
- Subtract: 6615−3515=3115=2115\frac{66}{15} – \frac{35}{15} = \frac{31}{15} = 2 \frac{1}{15}1566−1535=1531=2151.
This method is applied in calculations such as measuring distances, time intervals, or weights.
Subtracting Fractions with Whole Numbers
To subtract a fraction from a whole number, we first express the whole number as a fraction with the same denominator as the given fraction.
Steps:
- Change the whole number to a fraction with the same denominator as the fraction.
- Subtract the numerators without changing the denominator.
- Simplify if necessary.
Example:
6−586 – \frac{5}{8}6−85
- Express 6 as 488\frac{48}{8}848.
- Subtract: 488−58=438=538\frac{48}{8} – \frac{5}{8} = \frac{43}{8} = 5 \frac{3}{8}848−85=843=583.
This technique is applied in many real-life situations such as calculating remaining funds, distance, or ingredients in recipes.
Practice Problems
To solidify your knowledge of subtracting fractions, attempt to solve these problems:
- 910−410\frac{9}{10} – \frac{4}{10}109−104
- 712−16\frac{7}{12} – \frac{1}{6}127−61
- 5−255 – \frac{2}{5}5−52
- 358−1343 \frac{5}{8} – 1 \frac{3}{4}385−143
- 116−59\frac{11}{6} – \frac{5}{9}611−95
Resolving these issues will make you more confident with subtracting fractions effectively.
Frequently Asked Questions (FAQs)
Fractions are portions of something, and having a common denominator means the portions to be subtracted have the same quantity.
A negative fraction means that the first fraction is less than the second one. This can be applied in finance and calculation of temperature.
Yes, improper fractions have the same rules for subtraction as proper fractions. If necessary, convert the answer to a mixed fraction.
Convert the whole number to a fraction with the same denominator before you subtract.
Improper fractions can be rewritten as mixed numbers for easier reading.
Final Thoughts
Mastering the subtraction of fractions—whether they have like or unlike denominators, involve mixed numbers, or include whole numbers—is an essential skill in mathematics. By following the step-by-step methods outlined in this guide, you can confidently tackle fraction problems in academic and real-life situations, such as budgeting, cooking, and measuring distances. Practice regularly to strengthen your understanding and build confidence in working with fractions. With time and effort, subtracting fractions will become second nature!
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math. You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.













