Introduction
The term hexadecimal comes from the words “hexa” (six) and “deci” (ten), which together represent the base-16 number system. Unlike the decimal system, which uses digits 0–9, hexadecimal uses 16 symbols:
- 0–9 for values zero to nine
- A–F for values ten to fifteen (A=10, B=11, C=12, D=13, E=14, F=15)
This compact system is widely used in programming, memory addressing, digital circuits, and color codes in web design because it represents large numbers more efficiently than binary or decimal.
What are Hexadecimal Numbers?
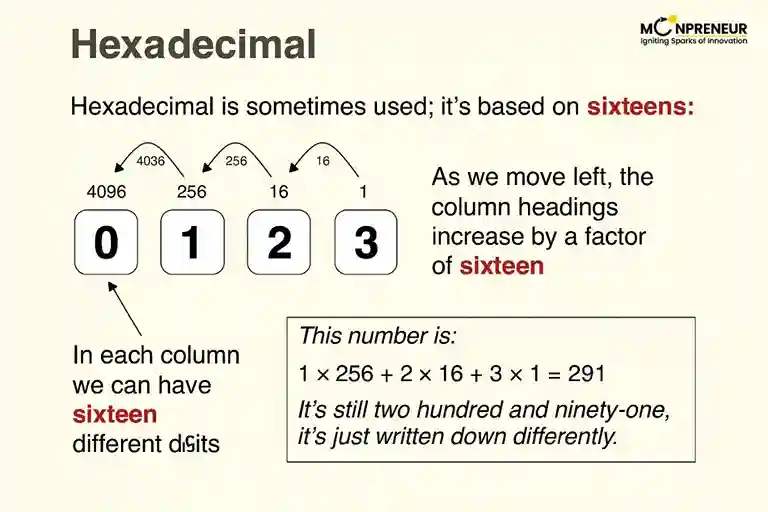
The hexadecimal number system is a positional system, where each digit’s position carries a value that is a power of 16. Each step left increases the weight by 16 times.
Example:
\(\displaystyle 2F_{16} = (2 \times 16^{1}) + (15 \times 16^{0}) = 32 + 15 = 47_{10}\)
This makes hexadecimal numbers extremely useful in simplifying binary codes.
Rules of Hexadecimal Addition
Hexadecimal addition follows the same principles as decimal addition but includes the extra symbols A–F.
- Write the numbers column by column.
- Add digits starting from the rightmost side.
- If the sum is less than 16, write it directly.
- If the sum is 16 or more, subtract 16 and carry 1.
- Replace values 10–15 with A–F.
Example:
\(\displaystyle B + 8 = 11 + 8 = 19 \;\;\Rightarrow\;\; 19 - 16 = 3, \; \text{carry 1}\)
Hexadecimal Addition Table
To make addition faster, here’s a useful hex addition table:
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
This table helps avoid manual decimal conversion when adding hex numbers.
Step-by-Step: How to Add Hexadecimal Numbers
Example 1: Add 3B1 + 26F
Ones place → \(\displaystyle 1 + F = 1 + 15 = 16 \;\;\to\;\; 0,\; \text{carry } 1\)
Tens place → \(\displaystyle B(11) + 6 = 17 + 1 = 18 \;\;\to\;\; 2,\; \text{carry } 1\)
Hundreds place → \(\displaystyle 3 + 2 + 1 = 6\)
Final Answer: \(\displaystyle 620\)
Example 2: Add 8AB + B78
Ones place → \(\displaystyle B + 8 = 11 + 8 = 19 \;\;\to\;\; 3,\; \text{carry } 1\)
Tens place → \(\displaystyle A(10) + 7 + 1 = 18 \;\;\to\;\; 2,\; \text{carry } 1\)
Hundreds place → \(\displaystyle 8 + B(11) + 1 = 20 \;\;\to\;\; 4,\; \text{carry } 1\)
Thousands place → \(\displaystyle 1 \text{ (carry left)}\)
Final Answer: \(\displaystyle 1423\)
Example 3: Add D6E + 8C6
Ones place → \(\displaystyle E(14) + 6 = 20 \;\;\to\;\; 4,\; \text{carry } 1\)
Tens place → \(\displaystyle 6 + C(12) + 1 = 19 \;\;\to\;\; 3,\; \text{carry } 1\)
Hundreds place → \(\displaystyle D(13) + 8 + 1 = 22 \;\;\to\;\; 6,\; \text{carry } 1\)
Thousands place → \(\displaystyle 1 \text{ (carry left)}\)
Final Answer: \(\displaystyle 1634\)
Applications of Hexadecimal Numbers
The hexadecimal system has several practical uses:
- Computer Programming: Used in assembly language and debugging.
- Memory Addressing: Represents large memory addresses compactly.
- Color Codes in Web Design: Colors are represented as hex values (e.g., #FF5733).
- Error Detection: Helps programmers trace errors in code.
Recommended Reading: What is 30% of 50?
Practice Problems
Test your understanding with these problems:
- Add 7D + 8E
- Add 9A + B7
- Add F9 + 27
- Add 1A3 + 2F7
- Add C5 + 3B
Answers: 10B, 151, 120, 49A, 100
Recommended Reading:
Conclusion
The hexadecimal number system is a compact, base-16 system widely applied in technology, computing, and electronics. Hexadecimal addition is simple once you understand the rules: add digit by digit, carry over when the sum exceeds 15, and replace values 10–15 with A–F. With practice and the help of the hex addition table, you can confidently solve problems and apply hexadecimal operations in real-world scenarios.
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle












