Update: This article was last updated on 4th December 2024 to reflect the accuracy and up-to-date information on the page.
Cubics are those intriguing mathematical expressions which involve the powers of three and can be extremely exhausting to solve sometimes. In this step-by-step guide, we’ll explain the formulas for a3−b3a^3 – b^3a3−b3 and a3+b3a^3 + b^3a3+b3 in an easy and approachable manner. These a3−b3a^3-b^3a3−b3 formula and a3+b3a^3+b^3a3+b3 formula simplify complex cubic expressions and are essential tools in algebra. Mastering these a^3 b^3 formula** equations, such as **\(a^3 – b^3 and the a3+b3a^3 + b^3a3+b3 formula, helps in reducing polynomials. Whether it’s the a3+b3a^3 + b^3a3+b3 formula or the a3−b3a^3 – b^3a3−b3 formula, this guide makes learning these expressions simple. Explore these a3_b3 formula concepts for a clearer understanding of algebraic operations.
In this blog, we’ll break down these formulas step-by-step, understand their derivation, and explore examples to help you master them.
Recommended Reading: Quotient of Powers
Difference of Cubes (a3 – b3):
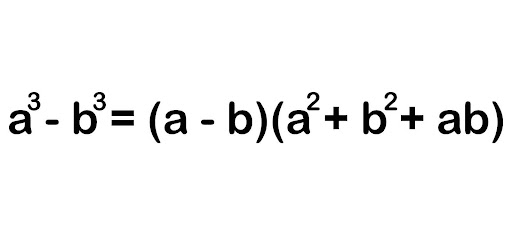
Step 1: Understand the Expression
Our journey begins with understanding the expression (a3 – b3).
Step 2: Recognize the Pattern
The formula for the difference of cubes is
a3 – b3 = (a – b)(a2 + ab + b2).
Step 3: Factorize
Now, let’s break down the expression into a product of a binomial and a trinomial:
(a – b)(a2 + ab + b2).
The difference of cubes is now neatly factorized.
Recommended Reading: What is the Derivative of sec x?
Sum of Cubes (a3 + b3):
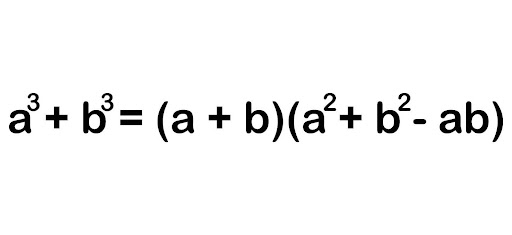
Step 1: Understand the Expression
Now, let’s explore (a3 + b3), this is the sum of two cubes.
Step 2: Recognize the Pattern
The formula for the sum of cubes is (a3 + b3 = (a + b)(a2 – ab + b2).
Step 3: Factorize
Just as we did before, break down the expression into a product of a binomial and a trinomial:
(a + b)(a2 – ab + b2).
The sum of cubes has now been transformed into a comprehensible and factorized form.
Key Differences Between a3−b3a^3 – b^3a3−b3 and a3+b3a^3 + b^3a3+b3
Conclusion:
By recognizing the patterns and applying factorization magic, these seemingly complex cubic expressions have been demystified. Armed with these formulas, you’re well-equipped to tackle cubic challenges with confidence and ease. Keep exploring the fascinating world of mathematics!
Mathematics is all about patterns, and formulas play a vital role in simplifying complex expressions. Among the most commonly used algebraic identities are the formulas for a3−b3a^3 – b^3a3−b3 and a3+b3a^3 + b^3a3+b3. These formulas are essential for solving polynomial equations, factoring expressions, and simplifying computations.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!
