Welcome to a detailed examination of the factors of 90. This article is tailored for those who are passionate about mathematics or simply curious about the numerical properties of 90.
We will break down the numbers that, when multiplied together, equal 90, making the concept of factors easy to grasp.
What Are the Factors of 90?
Factors of 90 are the numbers that, when multiplied in pairs, result in 90. These factors are vital to understanding how the number 90 is structured. For example, some pairs of factors are 1 and 90, 2 and 45, 3 and 30, among others.
Pair Factors of 90
The number 90 pair factors are sets of two numbers that result in 90 when multiplied together. This concept extends to both positive and negative pairs, as the multiplication of two negatives also yields a positive result.
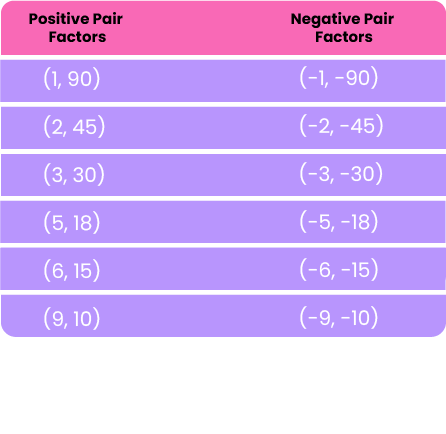
Positive and Negative Pair Factors of 90:
Here is a breakdown of the positive and negative pair factors of 90:
How to Find the Factors of 90?
To find the factors of 90, follow these steps:
1. Start with the Number One:
1 and 90 form the first factor pair since 1 multiplied by any number gives that number.
2. Examine Divisibility:
Check which numbers can be divided 90 evenly. For example, 2 times 45 and 3 times 30 are valid pairs.
3. Look at Square Roots:
Check numbers up to the square root of 90 for potential factors.
Include Negative Factors: Always include the negative counterparts for each positive factor.
Prime Factorization Method
Prime factorization involves deconstructing a composite number to its prime components, the fundamental prime numbers that, when multiplied, reconstruct the original number.
Prime factorization involves breaking down a number into its most minor prime number factors. The process for 90 is as follows:
1. Start with the Smallest Prime Number:
Begin with the smallest prime number that divides 90, which is 2.
2. Continue Dividing:
Divide 90 by 2 to get 45, then proceed with the following smallest prime number, 3. Keep dividing until only prime numbers remain.
3. List the Prime Factors:
The prime factorization of 90 is 2×32×5, with 2, 3, and 5 being prime numbers.
Summary
This comprehensive guide gives a clear understanding of the factors of 90. Discover how pairs like 1 and 90, 2 and 45, or 3 and 30, along with their negative counterparts, make up the structure of 90. Learn to identify these factors and understand the prime factorization of 90 as 2×32×5, which is essential for those interested in mathematics.
They not only deepen your mathematical understanding but also sharpen your problem-solving skills. Whether you’re in the classroom or facing real-world mathematical challenges, mastering these methods will undoubtedly prove beneficial.
Frequently Asked Questions on Factors of 90
Q1. What numbers constitute the factors of 90?
Ans: The factors of 90 are the numbers that when multiplied together, equal 90. These include 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Q2: How do I determine the factors of 90?
Ans: To find the factors of 90, start with 1 and gradually check which numbers divide 90 evenly without leaving any remainder.
Q3: Are there negative numbers that are factors of 90?
Ans: Yes, every positive factor of 90 has an equivalent negative counterpart. This means -1, -2, -3, -5, -6, -9, -10, -15, -18, -30, -45, and -90 are also factors of 90.
Q4: Could you explain the prime factorization for 90?
Ans: The prime factorization of 90 involves breaking it down into its most minor prime factors, which are 2, 3, and 5. Thus, the prime factorization of 90 is 2×32×5.
Q5: Do the factors of 90 have practical uses in daily activities?
Ans: Understanding the factors of 90 can be helpful in various practical situations, such as in organizing or grouping objects or in solving specific mathematical problems that involve division or multiplication.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course and Math Quiz for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!