In mathematics, understanding a function’s domain is crucial for analyzing its behavior and defining its limitations. The domain represents all input values for which the function is defined, ensuring meaningful output.
If this topic is new to you, explore it with us. In this blog, we will discuss how to determine it for various types of functions with examples.
WHAT IS THE DOMAIN OF A FUNCTION?
The domain of a function is the set of all permissible input values that can be used to evaluate the function. It defines the range of values over which the function is defined and produces valid results.
For instance, in the function f(x) = √x, the domain is x ≥ 0, indicating that only non-negative values of x are allowed.
Recommended Reading: THE IMPACT OF LIMITED PERSONAL ATTENTION ON CHILD’S MATH SKILLS
HOW TO FIND THE DOMAIN OF A FUNCTION
Let’s look at the step-by-step guide on how we can find the domain of any function.
Step 1: Look at the Function
First, you need to look at the function you have.
For example, let’s say we have a function like f(x) = x^2.
Step 2: Check for Restrictions:
Some functions have rules about what numbers we can use.
For example, if you have a function like g(x) = 1/x, you can’t put in the number 0 because you can’t divide by zero.
Step 3: Think about Square Roots:
If you have a function with a square root like h(x) = √x, remember that you can’t take the square root of a negative number.
Step 4: Consider Fractions:
If your function has fractions, remember that you can’t divide by zero. So, if you have a function like k(x) = 1/(x-2), you can’t use the number 2 because it would make the denominator zero.
Step 5: Put it All Together:
Once you’ve checked for these rules, you’ll have your domain – the numbers you can use in your function without breaking any math rules.
Recommended Reading: WHAT IS UNIT RATE? EXAMPLE AND FAQS
EXAMPLES
Function f(x) = x^2: The domain is all real numbers because you can square any number without any restrictions.
Function g(x) = 1/x: The domain is all real numbers except 0 because you can’t divide by zero.
Function h(x) = √x: The domain is all real numbers greater than or equal to 0 because you can’t take the square root of a negative number.
Function k(x) = 1/(x-2): The domain is all real numbers except 2 because you can’t divide by zero.
IIMPORTANCE OF DOMAIN AND RANGE
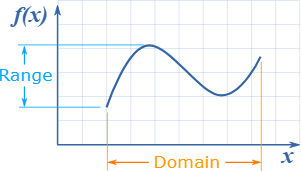
Understanding the domain and range of a function aids in graphing functions accurately, identifying discontinuities, holes, or asymptotes, and interpreting mathematical results effectively. The range complements the domain by representing all output values of the function.
In conclusion, the domain of a function is fundamental in mathematics, defining the valid input values for a function. By recognizing common restrictions and analyzing examples, one can proficiently determine the domain of various functions, enhancing mathematical comprehension and problem-solving skills.
By following this structure and incorporating detailed explanations and examples, you can create a comprehensive math blog on the domain of a function.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course and Math Quiz for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!












