Mastering the Quadratic Formula
We have all been there during a timed practice test: you stare at a quadratic equation like
ax² + bx + c = 0, and for a split second, the formula slips your mind. While most students know the solution involves \(\displaystyle x = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)
,understanding where it comes from and how is derived is better.
That is the logic of “Completing the square”
Recommended Reading: An overview of the SAT Math Test Sections
Let’s See it in Action: A Practical Example
Before diving into the abstract letters, let’s look at a real equation: 9x²+3x−2=0.
To solve this without just plugging numbers into a formula, you can transform it into a perfect square:
- Rewrite the first term: Think of 9x² as (3x)².
- Match the middle term: We want to fit the pattern \(\displaystyle a^{2} + 2ab + b^{2}\), to get 3x from 2⋅(3x)⋅b, our “b” must be ½.
Balance the equation: Add and subtract (1/2)², (which is 1/4), so the value doesn’t change.
- Simplify: This allows you to rewrite the equation as (3x+1/2)² −9/4=0.
By taking the square root of both sides, you find two solutions: x=1/3 and x=−2/3. This method proves that you can solve complex quadratics using basic algebraic balance.
Recommended Reading The Ultimate Guide to Solving SAT Quadratics in Seconds
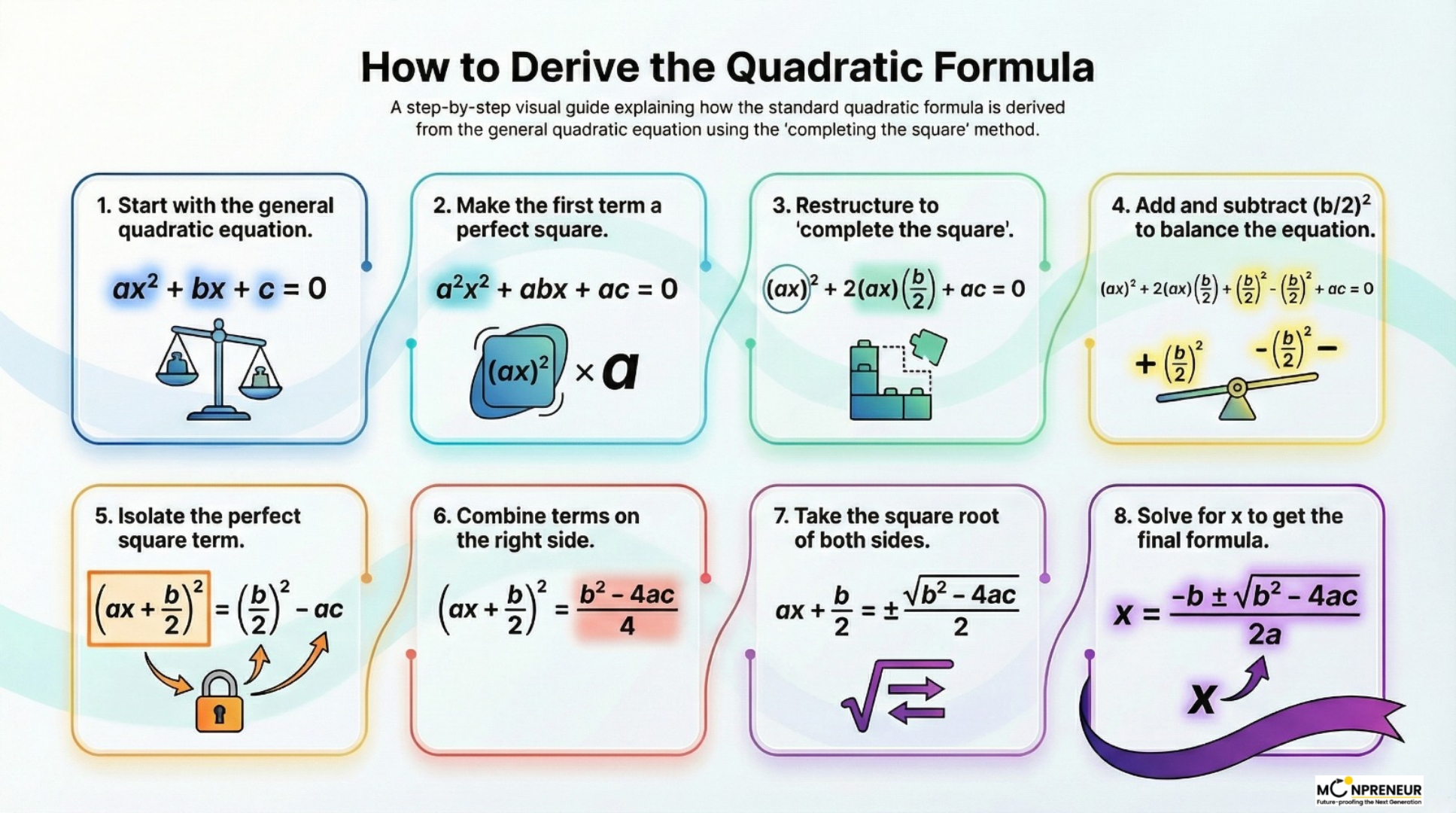
The famous quadratic formula is simply this same process applied to the general form ax² +bx+c=0.
- Multiply the whole equation by a to get a² x²+abx+ac=0.
- Complete the square by adding and subtracting (b/2)², which allows you to form the group (ax+b/2)².
- Isolate x by moving terms to the right-hand side and taking the square root.
- This results in the formula we all know: \(\displaystyle x = \frac{-b \pm \sqrt{b^{2} – 4ac}}{2a}\)
For a more detailed explanation, you can follow this video:
At the end of the day, maths is more about understanding the logic than just memorising a string of letters. By taking a moment to practise this derivation with a pencil and paper, you are building a mental tool that will stay with you long after the SAT is over. If you ever feel stuck or forget the exact formula, you can trust in your ability to use these steps to derive the solution yourself.
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.