Cube Root From 1 to 30
Cube roots are an essential part of learning mathematics, especially when you’re diving into algebra and geometry. Whether you’re a student, teacher, or parent helping your child, understanding cube roots from 1 to 30 lays a strong foundation for solving higher-level problems.
Let’s explore what cube roots are and how they work—along with a useful chart showing cube roots from 1 to 30.

What is a Cube Root?
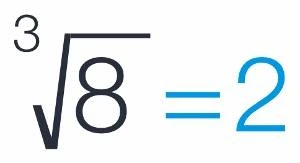
The cube root of a number is the value that, when multiplied by itself three times, results in the original number. In mathematical terms, the cube root of a number “x” is written as:
x³ = y ⇒ y × y × y = x
For example: ∛8 = 2, because 2 × 2 × 2 = 8
The cube root helps you work backward from a cube number to its original base.
Why Learn Cube Roots?
Cube roots are more than just a math exercise—they’re useful in real life too. Here’s why they matter:
- Used in volume calculations (e.g., finding side length of a cube).
- Important in algebra, geometry, and data science.
- Helpful in engineering, computer graphics, and game development.
Cube Root Chart from 1 to 30
Here’s a quick-reference chart showing the cube roots of numbers from 1 to 30. Some of them are whole numbers (perfect cubes), while others are approximated to three decimal places.
How to Write 27 in Roman Numerals?
To write 27 as a Roman numeral, break it down:
- 10 + 10 = XX
- 5 = V
- 1 + 1 = II
Put it all together: XX + V + II = XXVII
So, 27 in Roman numerals is XXVII.
Roman Numeral Chart (1–30)
| Number | Cube Root (∛n) | Approximate Value |
|---|---|---|
| 1 | ∛1 | 1.000 |
| 2 | ∛2 | 1.260 |
| 3 | ∛3 | 1.442 |
| 4 | ∛4 | 1.587 |
| 5 | ∛5 | 1.710 |
| 6 | ∛6 | 1.817 |
| 7 | ∛7 | 1.913 |
| 8 | ∛8 | 2.000 |
| 9 | ∛9 | 2.080 |
| 10 | ∛10 | 2.154 |
| 11 | ∛11 | 2.224 |
| 12 | ∛12 | 2.289 |
| 13 | ∛13 | 2.351 |
| 14 | ∛14 | 2.410 |
| 15 | ∛15 | 2.466 |
| 16 | ∛16 | 2.519 |
| 17 | ∛17 | 2.571 |
| 18 | ∛18 | 2.620 |
| 19 | ∛19 | 2.668 |
| 20 | ∛20 | 2.714 |
| 21 | ∛21 | 2.758 |
| 22 | ∛22 | 2.802 |
| 23 | ∛23 | 2.844 |
| 24 | ∛24 | 2.884 |
| 25 | ∛25 | 2.924 |
| 26 | ∛26 | 2.962 |
| 27 | ∛27 | 3.000 |
| 28 | ∛28 | 3.037 |
| 29 | ∛29 | 3.072 |
| 30 | ∛30 | 3.107 |
How to Calculate Cube Roots Easily
There are different ways to find cube roots:
1. Identify Perfect Cubes.
Numbers like 1, 8, and 27 are perfect cubes. You can easily find their cube roots without a calculator.
Examples:
- ∛1 = 1
- ∛8 = 2
- ∛27 = 3
2. Use Estimation or Calculator
For numbers like 9 or 20, which are not perfect cubes, use estimation or a calculator for the approximate value.
Example:
- ∛9 ≈ 2.080
- ∛20 ≈ 2.714
Quick Memory Tip: Perfect Cubes from 1³ to 10³
Memorize these to quickly spot perfect cubes:
- 1³ = 1
- 2³ = 8
- 3³ = 27
- 4³ = 64
- 5³ = 125
- 6³ = 216
- 7³ = 343
- 8³ = 512
- 9³ = 729
- 10³ = 1000
Applications of Cube Roots
- Education: Essential for students preparing for math Olympiads or competitive exams.
- Construction: Useful when calculating cube-shaped volume dimensions.
- Programming: Game developers and data scientists often deal with cube root formulas.
Conclusion
Learning the cube root from 1 to 30 helps build strong number sense. Whether you’re solving math puzzles, preparing for exams, or working on real-world problems, cube roots play a key role. Use the chart above for reference, practice identifying perfect cubes, and you’ll be a cube root pro in no time!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.













