Understanding Corresponding Angles in Geometry.

Updated: August 6, 2025

|

Category: Advance Math, Math

What are Corresponding Angles?

Corresponding angles are pairs of angles that occupy the same relative position at each intersection where a transversal crosses two lines. If two parallel lines are cut by a transversal, these angles appear in matching corners.

Example: Imagine two parallel lines being crossed by a slanting line. The angle formed on the top left of the first intersection and the top left of the second intersection are corresponding.

Understanding Corresponding Angles with Diagrams

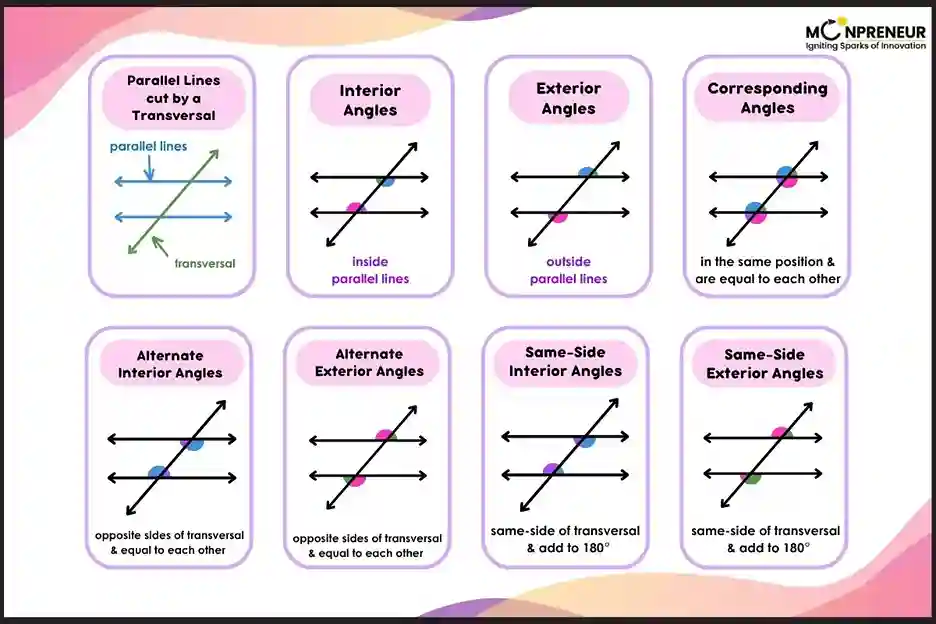
When a transversal cuts through two lines, it creates eight angles. Among them, four pairs are considered corresponding because they are in the same position at both crossings.

Types of Corresponding Angles

There are two main scenarios where corresponding angles are formed:

When the transversal intersects two parallel lines
When the transversal intersects two non-parallel lines

Let’s explore each case:

1. Corresponding Angles Formed by Parallel Lines

When two parallel lines are intersected by a transversal, each pair of corresponding angles is equal in measure.

Example:
Let’s say the transversal forms ∠a on the top left of the first intersection and ∠e on the top left of the second — since the lines are parallel: ∠a = ∠e

Pairs of Equal Corresponding Angles:

∠a = ∠e
∠b = ∠f
∠c = ∠g
∠d = ∠h

These angles are always congruent when the lines are parallel.

2. Corresponding Angles Formed by Non-Parallel Lines

When a transversal intersects non-parallel lines, the corresponding angles still occupy the same positions, but they are not necessarily equal.

This means:

∠a might not equal ∠e
∠b might not equal ∠f
and so on.

There is no special relationship between them unless the lines are confirmed to be parallel.

Other Angles Formed by a Transversal

Along with corresponding angles, several other angle types form when a transversal intersects two lines:

Angle Type	Definition	Angle Relationship
Corresponding Angles	Same position at each intersection	∠a = ∠e, ∠b = ∠f (if lines are parallel)
Vertically Opposite Angles	Angles directly across from each other at the intersection	∠a = ∠d, ∠b = ∠c, etc.
Alternate Interior Angles	Inside the parallel lines, on opposite sides of the transversal	∠c = ∠f, ∠d = ∠e
Alternate Exterior Angles	Outside the parallel lines, on opposite sides of the transversal	∠a = ∠h, ∠b = ∠g
Consecutive Interior Angles	Same side of the transversal and inside the lines, add up to 180°	∠c + ∠e = 180°, ∠d + ∠f = 180°

Corresponding Angles Theorem

The Corresponding Angles Theorem states:

If a transversal intersects two parallel lines, then each pair of corresponding angles is congruent.

Converse of the Corresponding Angles Theorem

The converse of the theorem goes like this:

If a transversal intersects two lines and the corresponding angles are congruent, then the two lines must be parallel. This is a helpful tool in geometry to prove that lines are parallel based on angle measures.

Corresponding Angles in Triangles

In the context of triangles, corresponding angles occur when two similar or congruent triangles are compared.

These angles:

Appear in matching positions within each triangle
Have equal measurements in both triangles

For example, if △ABC ∼ △XYZ, then ∠A = ∠X, ∠B = ∠Y, ∠C = ∠Z

Key Points to Remember

Corresponding angles lie in matching positions at the intersections formed by a transversal.
When the lines are parallel, corresponding angles are equal.
When the lines are not parallel, corresponding angles are not necessarily equal.
The Corresponding Angles Postulate helps prove angle relationships and parallelism in geometry.
In triangles, corresponding angles are equal if the triangles are similar or congruent.

Conclusion

Corresponding angles are a foundational concept in geometry, especially when studying angles formed by parallel lines and transversals. Whether you’re solving problems or proving theorems, recognizing corresponding angles and their properties makes things easier.

Next time you see lines and angles in math — or even in real life like railway tracks, bridges, or road intersections — try spotting those matching angle pairs!

Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!

You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.

Related Blogs:

$Moonpreneur$

Moonpreneur

Moonpreneur is an ed-tech company that imparts tech entrepreneurship to children aged 6 to 15. Its flagship offering, the Innovator Program, offers students a holistic learning experience that blends Technical Skills, Power Skills, and Entrepreneurial Skills with streams such as Robotics, Game Development, App Development, Advanced Math, Scratch Coding, and Book Writing & Publishing.