Introduction
In geometry, the circumradius of a triangle is the radius of the circle that passes through all three vertices of the triangle. This circle is called the circumcircle, and its center is known as the circumcenter. The circumradius plays an important role in trigonometry, coordinate geometry, and real-life applications such as navigation and engineering. In this blog, we’ll explore how to calculate the circumradius of different triangles with formulas and examples.
Circumradius Formula for Any Triangle
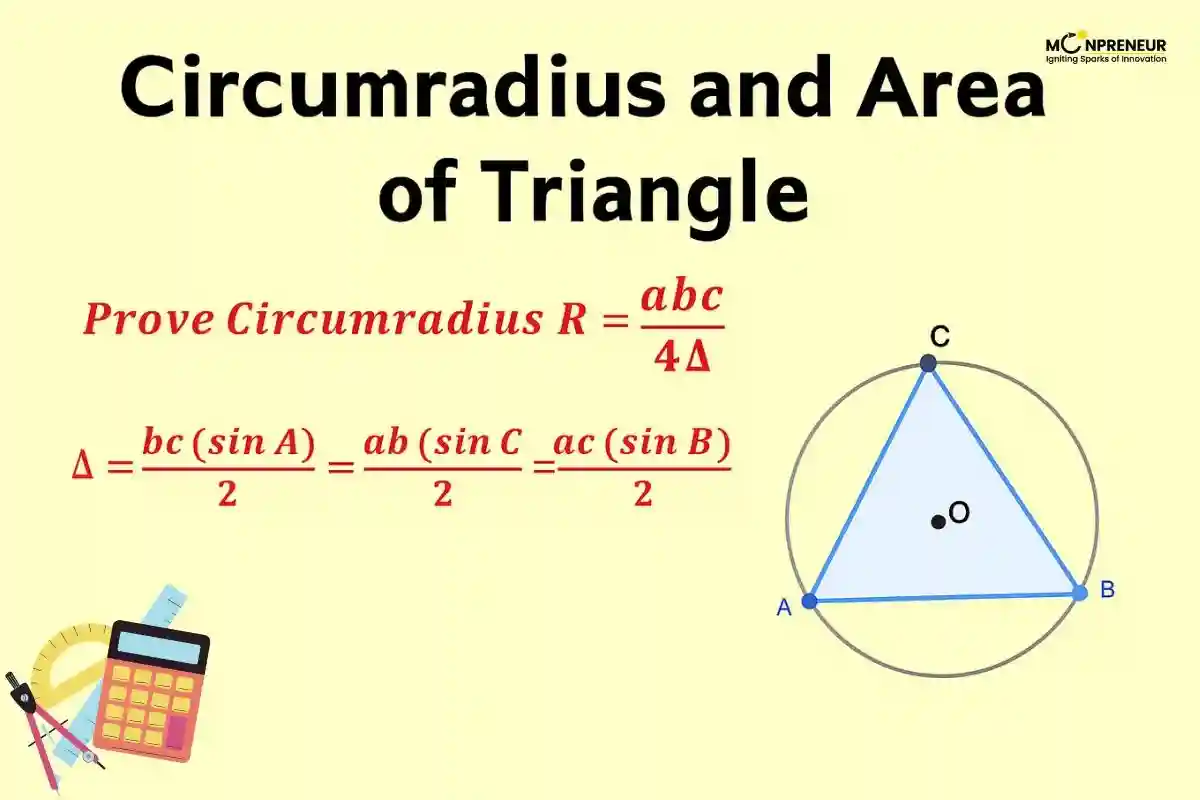
The general formula for the circumradius (R) of a triangle with sides a, b, and c, and area Δ is:
\(\displaystyle R = \frac{abc}{4\Delta}\)
Where:
→ a, b, c = sides of the triangle
→ Δ = area of the triangle (using Heron’s formula if needed)
This formula works for any triangle – scalene, isosceles, or equilateral.
Circumradius of a Right-Angled Triangle
For a right triangle, the hypotenuse acts as the diameter of the circumcircle. Therefore, the formula becomes:
\(\displaystyle R = \frac{\text{Hypotenuse}}{2}\)
Example: If the sides of a right triangle are 6 cm, 8 cm, and 10 cm, then:
\(\displaystyle R = \frac{10}{2} = 5 \,\text{cm}\)
Circumradius of an Equilateral Triangle
For an equilateral triangle with side length a:
\(\displaystyle R = \frac{a}{\sqrt{3}}\)
Example: For side a = 6:
\(\displaystyle R = \frac{6}{\sqrt{3}} = 2\sqrt{3} \,\text{cm}\)
Steps to Find Circumradius of a Triangle
1. Identify the type of triangle (scalene, right, or equilateral).
2. Use the corresponding formula:
– General: \(\displaystyle \frac{abc}{4\Delta}\)
– Right triangle: \(\displaystyle \frac{\text{Hypotenuse}}{2}\)
– Equilateral triangle: \(\displaystyle \frac{a}{\sqrt{3}}\)
3. Calculate the area if required using Heron’s formula:
\(\displaystyle \Delta = \sqrt{s(s-a)(s-b)(s-c)}\) ,
where \(\displaystyle s = \frac{a+b+c}{2}\) is the semi-perimeter.
4. Substitute values into the formula.
Example Problem
Find the circumradius of a triangle with sides 7 cm, 8 cm, and 9 cm.
Step 1: Find the semi-perimeter:
\(\displaystyle s = \frac{7+8+9}{2} = 12\)
Step 2: Find the area using Heron’s formula:
\(\displaystyle \Delta = \sqrt{12(12-7)(12-8)(12-9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} = 12\sqrt{5}\)
Step 3: Apply the formula:
\(\displaystyle R = \frac{7 \times 8 \times 9}{4 \times 12\sqrt{5}} = \frac{504}{48\sqrt{5}} = \frac{10.5}{\sqrt{5}} \approx 4.69 \,\text{cm}\)
So, the circumradius is approximately 4.69 cm.
Conclusion
Finding the circumradius of a triangle depends on the type of triangle and the available information. The universal formula is \(\displaystyle \frac{abc}{4\Delta}\) , but simpler forms exist for right-angled and equilateral triangles. By mastering this concept, students can solve geometry and trigonometry problems more efficiently.
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Frequently Asked Questions (FAQs)
Ans: The circumradius is the radius of the circle that passes through all three vertices of a triangle.
Ans: No, it depends on the type of triangle – different formulas apply for equilateral, right, and scalene triangles.
Ans: Yes, for right and equilateral triangles, you can directly use simplified formulas.
Ans: It is useful in trigonometry, circle geometry, navigation, and in constructing geometric models.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle













