Update: This article was last updated on 28th January 2025 to reflect the accuracy and up-to-date information on the page.
An axis of symmetry is a line that can cut a splits a shape into two half parts such that if you were viewing the shape from this line, the two half parts would appear as if they were mirror images. You may also fold the shape along this line; the two parts will match. The axis of symmetry is very important in mathematics as it explains different shapes, equations, and graphs. This meaning extends into deeper axes of symmetry, representing different lines that might be obtained in a certain geometric shape. An axis of symmetry formula would, therefore, be essential in finding the line of symmetry for the parabola using algebraic functions.
An example of when to use such an equation is where one wants to find how to use the formula to solve for axis of symmetry with the quadratic formula as given by: x=−b2ax = -\\frac{b}{2a}x=−2ab.
One common axis of symmetry example is the vertical line through the vertex of a parabola, which is expressed by the axis of symmetry equation. Symmetry is also present in many everyday objects, so symmetry examples are easy to find. At times, even shapes or graphs may have a horizontal axis of symmetry, as is the case for some quadratic or higher-degree equations. We will learn more about the axis of symmetry and how to use it in different situations.
What is Symmetry
Some things look the same on both sides. This is called symmetry. Symmetry often involves an axis of symmetry, which is an imaginary line that divides a shape into two equal parts. You can see symmetry in nature, art, and buildings. For example, a flower or a butterfly has symmetry. The axis of symmetry formula helps in finding this line of division, and learning how to find the axis of symmetry can be very useful in various fields. You can draw a line in the middle of them, and the two sides will look the same. Symmetry makes things look nice and balanced.
For example, many paintings and buildings have symmetry. In some cases, objects may have multiple axes of symmetry, meaning they can be divided evenly in more than one way, such as through a horizontal axis of symmetry. People have been studying symmetry for a long time. Symmetry examples are abundant in daily life and are helpful in many fields, such as engineering, physics, and chemistry.
There are many different types of symmetry, including:

Reflectional symmetry
This is the simplest way of explaining symmetry. Symmetry examples show that something can be divided into two equal parts and they look alike. For example, a square is symmetrical since you can fold it in half along any of its sides, and the two pieces will look identical. The line along which you can fold the shape to make the two parts match is called the axis of symmetry.
Symmetry makes things look nice and balanced. The axes of symmetry meaning refers to multiple lines of symmetry, like in a circle, which has infinite lines of symmetry. For a parabola, the axis of symmetry formula helps determine the line that divides the graph into two mirror images. To understand how to find the axis of symmetry, use the formula or observe the shape’s properties. Another type of an axis of symmetry is the vertical line that can be drawn and cuts a parabola in two equal halves. In other instances, you might have the horizontal axis of symmetry depending on the shape or equation. An axis of symmetry equation can therefore be found using a study of either geometric or algebraic properties of an object.
Rotational symmetry
This is a second way that could explain symmetry. It means that something can be turned around a point or line-called an axis of symmetry-and still look the same. For example, you can turn a circle around its center by any amount, and it will not change. A line in geometry is considered to be an axis of symmetry if the shape is divided into two identical parts.
For example, the parabola has a horizontal axis of symmetry that keeps it balanced on both sides. Symmetry is what makes things look nice and balanced. The formula to find the axis of symmetry is in the form of x=−b/2ax = -b/2ax=−b/2a for a quadratic equation. Other examples of shapes with symmetry are squares, triangles, and circles. Most of the time, they have one or more axes of symmetry.
Translational symmetry
This refers to another explanation for symmetry. It means something can be slid along a line, called the axis of symmetry, and still look the same. For example, a line is symmetric since you may slide it along and it will not change. This is a balance line because if you divide a shape into two identical parts that look the same on either side.
Symmetry is what makes things look nice and balanced. There are also many examples of symmetry, like butterfly wings and many geometric shapes. To better understand the meaning of axes of symmetry, let’s consider a parabola in mathematics. Its formula for the axis of symmetry helps locate that line which splits it into equal parts. If one wants to know how to find the axis of symmetry, it is often found through an equation, like the equation of the axis of symmetry for a quadratic function. Shapes can also be provided with a horizontal axis of symmetry, like a rectangle or an ellipse, that adds to its balanced look.
Types of Axes of Symmetry
The axis of symmetry is the line that gives a shape an appearance of the same on both sides. The two sides will match up if you fold the shape along this line. Understanding the meaning of axes of symmetry can help us learn more about shapes and how they are made. There are different kinds of axes of symmetry, such as the horizontal axis of symmetry, which plays an essential role in understanding shape properties. Using the axis of symmetry formula, we can calculate and determine the line of symmetry for different figures. It is very important in geometry to know how to locate the axis of symmetry.
For example, folding a square along one of its diagonals is an example of an axis of symmetry. The equation of an axis of symmetry also enables us to make mathematically exact calculations involving graphs and functions. Looking at some real-world symmetry examples further appreciates the nature and art balanced designs.
Axis of Symmetry Formula for Vertical:
It’s a line that travels up and down the middle of a shape, dividing it into two parts, which look to be mirror images of each other. Such a line is referred to as an axis of symmetry. For example, the letter “A” has a vertical axis of symmetry. To understand further, the axes of symmetry meaning defines how shapes may be divided symmetrically.
Additionally, the axis of symmetry formula helps determine this line mathematically. Learning how to find the axis of symmetry is essential in geometry. An axis of symmetry example can also be found in shapes like circles or rectangles. The axis of symmetry equation is another tool for precise calculations. Other symmetry examples include the butterfly’s wings and human faces. In some instances, there might also be a horizontal axis of symmetry just like in the letter “B“ or “8.”
Horizontal Axis of Symmetry:
This is the line that is called the axis of symmetry. It passes through the middle of the shape going left and right. It divides the shape into two parts that can be regarded as mirror images of one another. For example, the letter “H” has a horizontal axis of symmetry.
The axes of symmetry meaning in geometry and algebra are crucial, since the axis of symmetry formula is widely used to calculate balance in figures. Finding how to get the axis of symmetry simplifies solving equations. A good axis of symmetry example is a parabola’s vertex. Many symmetry examples make use of the reflection line as described by the axis of symmetry equation, which makes it a critical concept in math.
Diagonal Axis of Symmetry:
It is a line that passes at an angle through the middle of a shape. It divides the shape into two parts, which are mirror images of each other. For instance, a triangle has three diagonal axes of symmetry, one for each side. The axis of symmetry is a fundamental concept in geometry that helps to understand balance and reflection in shapes. This concept is best understood through the determination of how one would divide a shape to make two equal parts. Axis of symmetry formulas are commonly applied in algebra to identify a line of symmetry for a parabola or another geometric figure. One should understand the method for locating an axis of symmetry as part of their mathematics training, since knowing these can make problems involving symmetry solvable.
The best example of an axis of symmetry is a circle. Any line passing through its center is the axis. The same can be said of the equation of the axis of symmetry for a parabola – it is how one finds a precise location of a parabola. Symmetry examples in both two-dimensional and three-dimensional figures are important. A parabola can have its axis of symmetry as horizontal or vertical, according to its position.
How to find the axis of symmetry for a parabola
Axis of Symmetry for a Parabola:
The axis of symmetry for a parabola is a vertical line that divides the parabolic curve into two symmetrical halves. It passes through the vertex of the parabola and is always a vertical line due to the nature of quadratic functions.
Formula: The formula to find the axis of symmetry for a parabola is:
x = -b / (2a)
Here, “a“ denotes the coefficient of the x^2 term of the quadratic equation and “b“ is the coefficient of the x term.
Example:
Now consider the quadratic equation y = 2x^2 + 4x – 3. The formula used to find the axis of symmetry of the quadratic is as follows.
nx = -b / (2a)
In the above equation a = 2 and b = 4.
Putting these values, we get:
x = -(4) / (2 * 2) = -4 / 4 = -1
Therefore, the axis of symmetry for the given parabola is x = -1. Which indicates that a line x = -1 halves the graph of a parabola into two symmetrical halves.
Method to find axis of symmetry Of quadratic function.
How to find the axis of symmetry For a quadratic function
Axis of Symmetry for a Quadratic Function:
The axis of symmetry for a quadratic function is the same as the axis of symmetry for a parabola. A vertical line divides the quadratic graph into two symmetrical parts.
Formula: The formula to find the axis of symmetry for a quadratic function is the same as for a parabola: x = -b / (2a)
Here, “a” represents the coefficient of the x^2 term in the quadratic function, and “b” represents the coefficient of the x term.
Example:
Consider the quadratic function f(x) = -3x^2 + 6x + 2. To determine the axis of symmetry, we can use the formula:
x = -b / (2a)
In this function, a = -3 and b = 6. Plugging these values into the formula, we get:
x = -(6) / (2 * -3) = -6 / -6 = 1
Therefore, the axis of symmetry for the given quadratic function is x = 1. This implies that the line x = 1 divides the quadratic graph into two symmetrical halves.
The axis of symmetry for both a parabola and a quadratic function is a vertical line that divides the graph into two symmetric parts. The formula x = -b / (2a) is used to calculate the x-coordinate of the axis of symmetry, where “a” and “b” are the coefficients of the quadratic equation or function.
Examples of axes of symmetry in geometry:
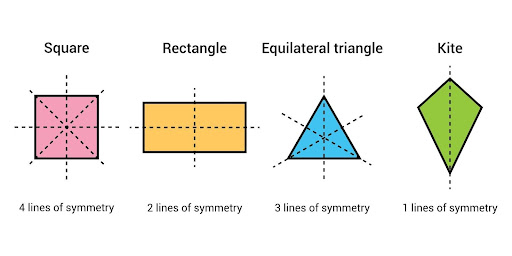
An axis of symmetry is a line that cuts a shape into two parts that are the same. Some shapes have more than one axis of symmetry, like squares, circles, and triangles with equal sides. Knowing about axes of symmetry helps us study how shapes are balanced.
Here are some example axes of symmetry in geometry
Square:
A square has four axes of symmetry. They are lines that connect the midpoints of opposite sides, forming two pairs of parallel lines that intersect at right angles.
Rectangle:
A rectangle has two axes of symmetry. They are lines that connect the midpoints of opposite sides and are parallel to the shorter sides of the rectangle.
Circle:
A circle has an endless number of axes of symmetry. Any line going through the center of the circle may be an axis of symmetry. Also, any diameter of the circle is an axis of symmetry.
Triangle:
Equilateral Triangle: Equilateral triangle has three axes of symmetry. They are lines connecting each vertex to the midpoint of the opposite side.
Isosceles Triangle:
An isoceles triangle is one with an axis of symmetry. The line divides the triangle in half into two congruent parts by bisecting the base.
Scalene Triangle:
A scalene triangle has no axes of symmetry because all sides and angles of a scalene triangle are different.
Real Life Applications of Axis of Symmetry
- The Taj Mahal and the Parthenon are good examples of architectural symmetries. They are impressive and solid.
- Nature‘s flower wonders, sunflowers and orchids, are examples of radial symmetry, hence harmonious designs that attract.
- Animals like butterflies and peacocks reflect bilateral symmetry with their mirrored features and exquisite designs.
- Crystals and minerals such as quartz and diamonds have highly intricate symmetrical patterns that can mesmerize our eyes with geometric precision.
In all these realms, the axis of symmetry shows inherent balance and beauty across our world, captivating and inspiring us in countless ways.
Summary
This article provides a concise and informative explanation of the axis of symmetry, along with the axes of symmetry meaning in mathematics. It encompasses concepts about symmetry, which includes examples of symmetry examples and the various types of symmetry such as the horizontal axis of symmetry, among others, and their applications in other fields. The article also discussed the formula of the axis of symmetry on how to determine the axis of symmetry with easy steps. Moreover, it encompasses practical examples on the axis of symmetry, explaining how to obtain the equation of the axis of symmetry for parabolas, quadratic functions, and geometric shapes.
Moonpreneur knows what this world of rapidly changing technology is in store for our kids. This course of advanced math, tailored by experts to grade 3rd, 4th, 5th, and 6th, would make your child develop his mathematical skills through the lesson’s hands-on learning approach, inspire him to learn, and prepare real-life applications for him.
Sign up today for a free 60-minute Advanced Math Workshop!














I remember a long time when I was really struggling with this concept of symmetry, especially concerning geometry. Everything became clear and sensible once I grasped how an axis of symmetry works. Such a helpful tool in solving equations and visualizing shapes better.
Symmetry is just so interesting! I see it used in everything from the work of artists to engineers. Have you ever noticed how often we use it without even realizing it in daily life?