The area of an isosceles triangle represents the region enclosed within the triangle in a two-dimensional plane. In simple terms, it tells us how much surface the triangle covers. Just like any other triangle, the area is measured in square units (cm², m², in², etc.). Since an isosceles triangle has two equal sides, its structure makes it easier to calculate the area using specific formulas.
What is an Isosceles Triangle?
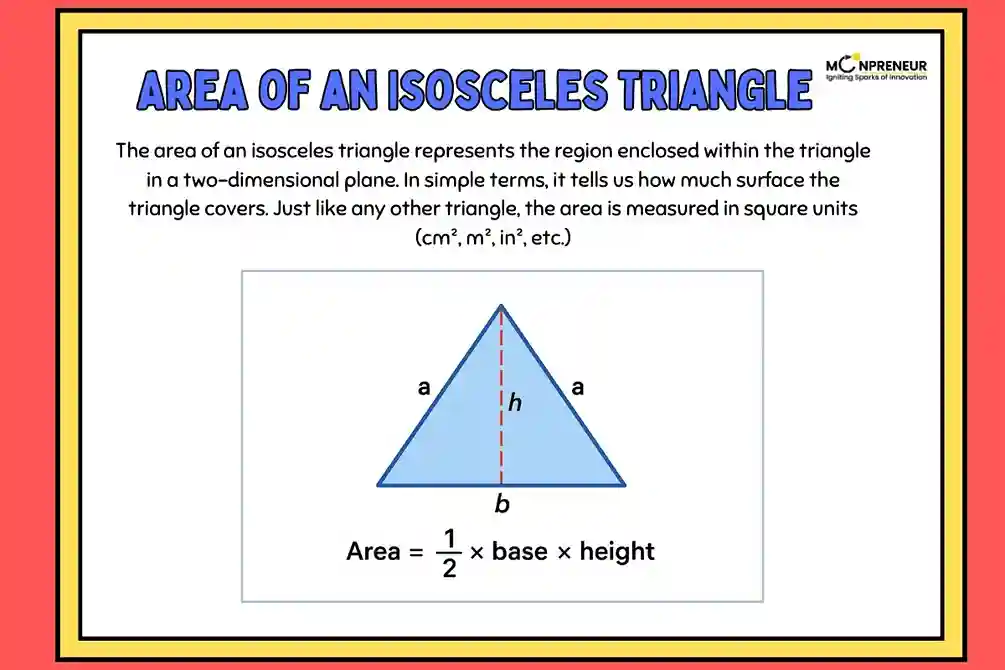
An isosceles triangle is a special type of triangle that has two equal sides and two equal angles. The third side is usually called the base, and the altitude (height) is the perpendicular line drawn from the vertex opposite the base.
Key Properties of an Isosceles Triangle:
- Two equal sides
- Two equal angles
- The altitude from the vertex to the base bisects the base
- An equilateral triangle is a special case of an isosceles triangle
Formula for the Area of an Isosceles Triangle
The most common formula is:
\(\mathrm{Area} = \frac{1}{2} \times \mathrm{base} \times \mathrm{height}\)List of Useful Formulas
- Using Base and Height: \(A = \frac{1}{2} \times b \times h\)
- Using Only Side Lengths: \(A = \frac{b}{4} \times \sqrt{4a^{2} – b^{2}}\)
- Using Trigonometry (two sides and included angle): \(A = \frac{1}{2} \times a \times b \times \sin(\alpha)\)
- For Isosceles Right Triangle: \(A = \frac{1}{2} \times a^{2}\)
How to Calculate Area – Step by Step
- Identify the base and equal sides of the triangle.
- If height is not provided, calculate it using: \(h = \sqrt{a^{2} – \frac{b^{2}}{4}}\)
- Apply the formula \(\frac{1}{2} \times b \times h\)
- Express the answer in square units.
Derivation Using Heron’s Formula
For a triangle with sides a, a, b:
\(s = \frac{a + a + b}{2} = \frac{2a + b}{2}\)
\(\text{Area} = \sqrt{s(s-a)(s-a)(s-b)}\)
Simplifying: \(\text{Area} = \frac{b}{2} \times \sqrt{a^{2} – \frac{b^{2}}{4}}\)
Area of an Isosceles Right Triangle
In an isosceles right triangle, the two equal sides are perpendicular.
\(\text{Area} = \frac{1}{2} \times a^{2}\)\(\text{Perimeter} = a(2 + \sqrt{2})\)
Solved Examples
Example 1:
Find the area of an isosceles triangle with base = 12 cm and height = 10 cm.
Solution: \(\text{Area} = \frac{1}{2} \times 12 \times 10 = 60 \,\text{cm}^2\)
Example 2:
Two equal sides = 13 cm, base = 10 cm. Find the area.
Solution: \(\text{Area} = \frac{10}{4} \times \sqrt{4 \times 13^{2} – 10^{2}} = 60 \,\text{cm}^2\)
Example 3:
Find the perimeter and area of an isosceles triangle with equal sides = 8 cm and base = 6 cm.
Solution: \(\text{Perimeter} = 22 \,\text{cm}, \quad \text{Height} \approx 7.41 \,\text{cm}, \quad \text{Area} \approx 22.23 \,\text{cm}^2\)
- Find the area of an isosceles triangle with base = 18 cm and height = 15 cm.
- An isosceles triangle has two equal sides of 10 cm each and base 12 cm. Find its area.
- Find the area of an isosceles right triangle with side 7 cm.
- The perimeter of an isosceles triangle is 42 cm. If the base is 12 cm, find its area.
Conclusion
The area of an isosceles triangle can be calculated easily using different formulas depending on the information available, such as the base and height, or the lengths of the sides. Understanding these methods not only improves mathematical skills but also helps in solving geometry problems in real life. By practicing with examples, students can confidently master the concept of finding the area of an isosceles triangle and apply it in higher-level mathematics.
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle
Frequently Asked Questions (FAQs)
A. \(\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}\)
A. \(h = \sqrt{a^{2} – \frac{b^{2}}{4}}\)
A. \(\text{Area} = \frac{1}{2} \times a^{2}\)
A. Perimeter = 2a + b.
A. They are used in architecture, roof designs, bridges, and art patterns.













