Angle Between Two Vectors: Definition, Formula & Examples
Understanding the angle between two vectors is an important concept in both mathematics and physics. Whether you’re working on vector algebra, computer graphics, or motion problems, this topic helps calculate how two vectors relate in direction.
In this blog, we’ll explore what the angle between two vectors means, how to calculate it, and where it applies in real life.
What is the Angle Between Two Vectors?
The angle between two vectors refers to the smallest angle formed when the two vectors are placed tail-to-tail. This angle tells us how much one vector must rotate to point in the direction of the other.
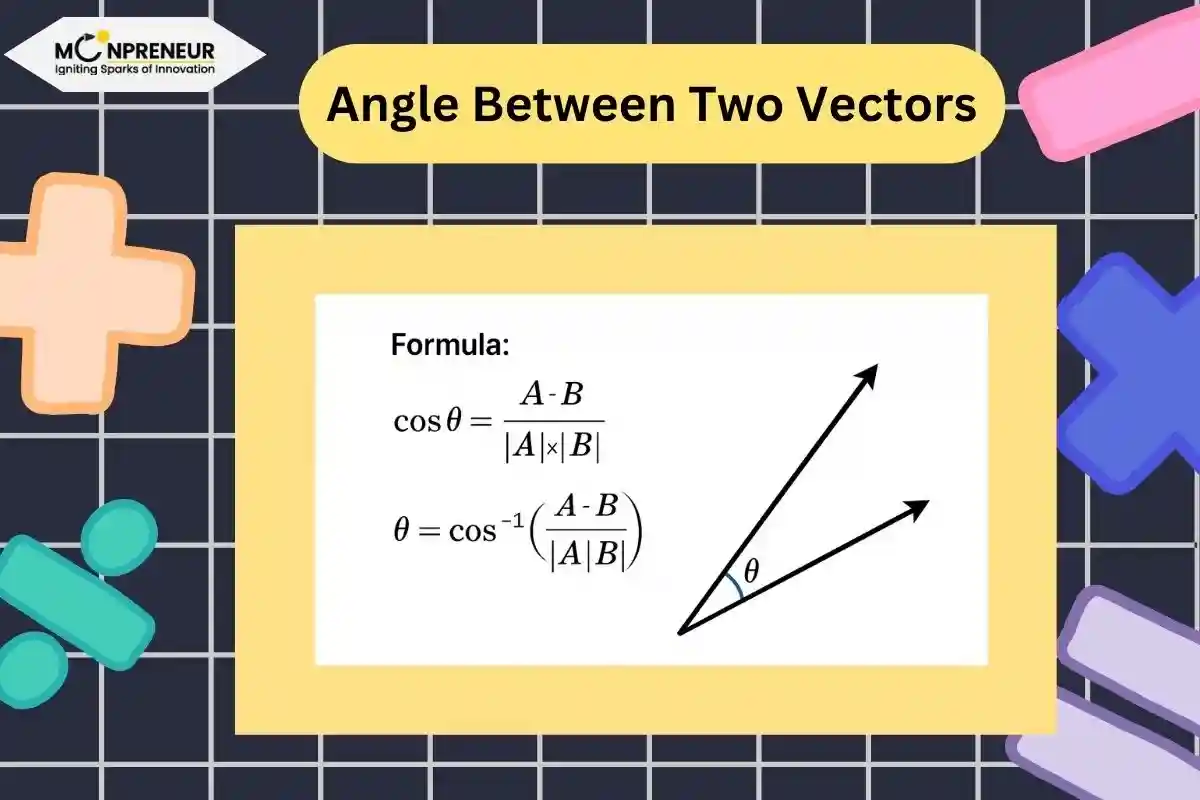
Formula to Find the Angle Between Two Vectors
To find the angle (θ) between two vectors A and B, use the following formula:
cos(θ) = (A • B) / (|A| × |B|)
Where:
- A • B is the dot product of vectors A and B
- |A| is the magnitude (length) of vector A
- |B| is the magnitude of vector B
- θ is the angle between the vectors
To find the angle θ in degrees or radians, use:θ = cos⁻¹ [(A • B) / (|A| × |B|)]
Step-by-Step Example
Let’s say:
Vector A = [2, 3]
Vector B = [4, 1]
Step 1: Find the dot product (A • B):
A • B = (2 × 4) + (3 × 1) = 8 + 3 = 11
Step 2: Find the magnitude of each vector:
|A| = √(2² + 3²) = √(4 + 9) = √13
|B| = √(4² + 1²) = √(16 + 1) = √17
Step 3: Plug into the formula:
cos(θ) = 11 / (√13 × √17)
Step 4: Use a calculator to find the angle:
θ = cos⁻¹ [11 / (√13 × √17)] ≈ 44.41°
Important Notes
- The angle is always between 0° and 180°
- If the dot product is 0, the vectors are perpendicular
- If the angle is 0°, the vectors are in the same direction
- If the angle is 180°, they are in opposite directions
Real-Life Applications
Understanding the angle between two vectors is useful in:
- Physics: analyzing forces and motion
- Engineering: calculating stress and tension
- Computer graphics: determining light reflection angles
- Robotics: adjusting movement between limbs and joints
Quick Summary Table
| Term | Meaning |
|---|---|
| Dot Product | A • B = a₁×b₁ + a₂×b₂ |
| Magnitude | ‖A‖ = √(a₁² + a₂²), ‖B‖ = √(b₁² + b₂²) |
| Angle Formula | θ = cos⁻¹ [(A • B) / (‖A‖ × ‖B‖)] |
| Angle Range | 0° ≤ θ ≤ 180° |
🌟 Final Thoughts
The angle between two vectors is a powerful tool in geometry, algebra, and physics. By understanding the dot product and vector magnitudes, students can master this essential concept with confidence. Practice a few problems on your own, and soon this will become second nature!
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle













