A Guide to the Leibniz Rule: Differentiating Under the Integral Sign

Hello Students, if you are preparing for the SAT or looking ahead to competitive exams, you know that calculus often feels like a series of complicated rules. But what if I told you there’s a “shortcut” that makes the most intimidating problems look easy?

Today, we’re diving into the Leibniz Rule, also known as Differentiation Under the Integral Sign. This is a favorite for examiners because it looks scary, but with a simple three-step process, you can master it in minutes.

What is the Leibniz rule?

Usually, when you see an integral, you think about finding the area under a curve. But sometimes, you aren’t asked to solve the integral—you are asked to find the derivative of that integral.

This gets tricky when the limits of the integral (the numbers at the top and bottom) are actually functions of x, like x² or x/2. The Leibniz Rule is the specific tool designed to handle these cases where the integration is done with respect to one variable (like t), but the derivative is taken with respect to another (like x).

The Leibniz Integral Rule (or Feynman’s Technique) evaluates complex definite integrals by differentiating under the integral sign with respect to a parameter. It allows swapping the order of derivation and integration

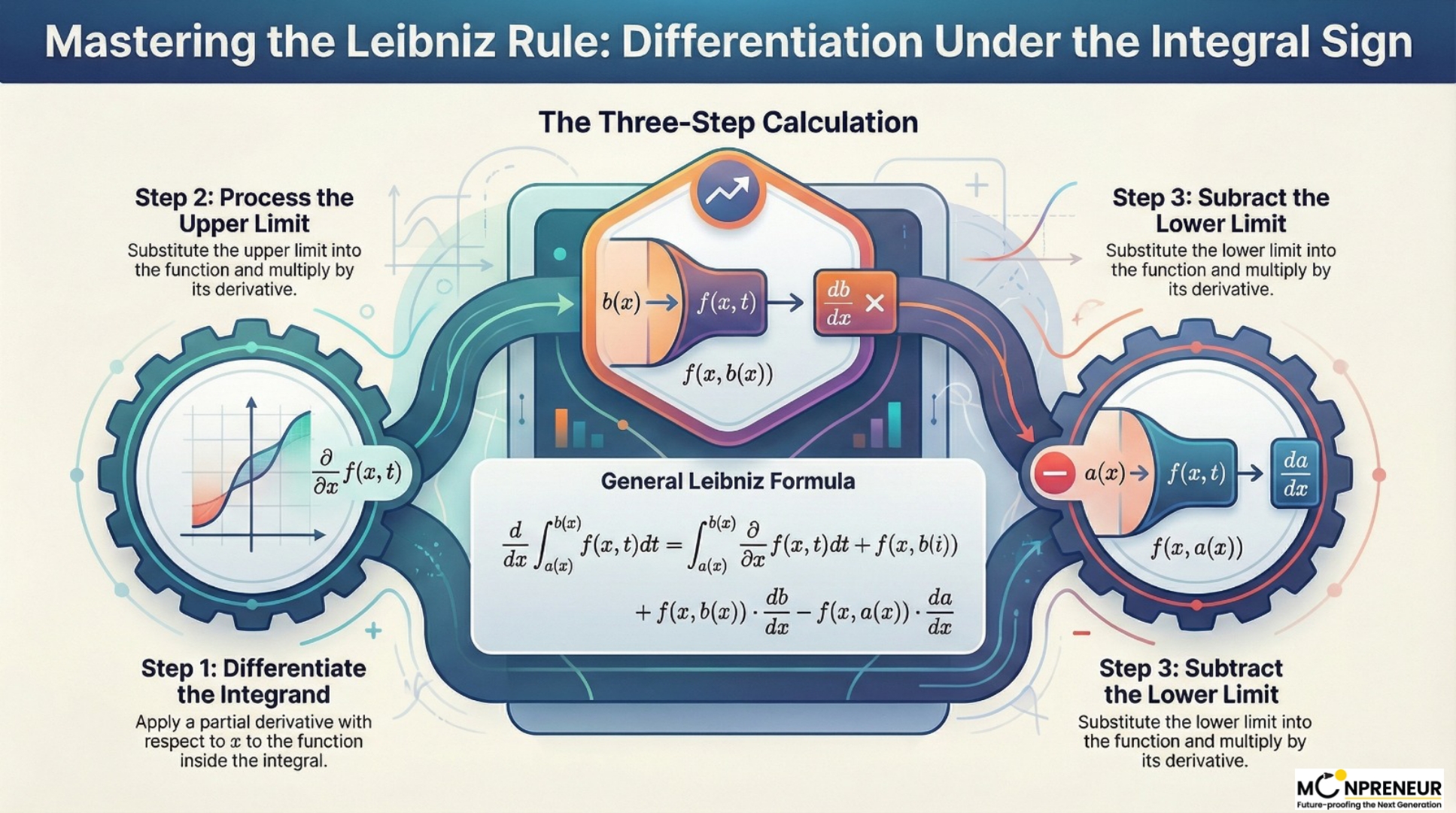
The General Formula

The Leibniz Rule handles cases where both the integrand and the limits of integration are functions of the same variable (usually t or x).

If we define a function I(t) as:

\(\displaystyle I(t) = \int_{a(t)}^{b(t)} f(x,t)\,dx\)

Then the derivative with respect to t is:

\(\displaystyle
\frac{d}{dt} I(t)
= \int_{a(t)}^{b(t)} \frac{\partial}{\partial t} f(x,t)\,dx
+ f(b(t),t)\, b'(t)
– f(a(t),t)\, a'(t)
\)

Breaking Down the Components:

• The Integral Term: You take the partial derivative of the inside function with respect to t.
• The Upper Limit Term: Evaluate the function at the upper limit and multiply by the derivative of that limit.
• The Lower Limit Term: Evaluate the function at the lower limit and multiply by the derivative of that limit (subtracted).

The 3-Step “Magic” Formula

1. Differentiate the “Inside”: Start by taking the partial derivative of the function inside the integral (the integrand) with respect to x.
2. Plug in the Upper Limit: Take your upper limit, substitute it into the function in place of t, and then multiply that result by the derivative of the upper limit itself.
3. Subtract the Lower Limit: Do the exact same thing for the lower limit—substitute it into the function and multiply by its derivative. Then, subtract this from your result in Step 2

When to use it

You should use this rule in two conditions:

1. Solving definite integrals: When an integral looks impossible (like \(\displaystyle \int \frac{\sin x}{x}\,dx\) , you can introduce a new variable t, differentiate, solve a simpler integral, and then integrate back.
2. Physics & Engineering: When dealing with moving boundaries (like a fluid flowing through a shrinking pipe) or time-varying fields. 

Why do we need it

Sometimes, the function inside the integral is impossible or very difficult to integrate directly. For example, if you have an integral of \(\displaystyle \sin^{-1}(t)\) from x/2 to 2x, finding the antiderivative first would be a nightmare. The Leibniz Rule allows you to bypass the integration entirely and go straight to the derivative!

Example of Leibniz’s rule

Solution:

Step 1: Differentiate the inside  

\(\displaystyle \frac{\partial}{\partial x}\cos(t^{2} + x) = -\sin(t^{2} + x)\)

Step 2: Apply the upper limit

Substitute t = x² into the function and multiply the derivative of x² (which is 2x).

Result: cos((x²)² + x) ⋅ 2x = 2x cos((x²)² + x) 

Step 3: Apply the lower limit

The limit is 0, and the derivative of 0 is 0. This term vanishes.

Final Answer: 

\(\displaystyle
G'(x) = \int_{0}^{x^{2}} -\sin(t^{2} + x)\,dt + 2x\cos(x^{4} + x)
\)