How to Use the Queen’s Property in Integrals

We’ve all been there. You’re looking at a definite integral that looks like a giant, tangled knot of sines, cosines, and fractions. It’s intimidating, it’s messy, and your first instinct might be to reach for a calculator.

But what if I told you there’s a “royal” shortcut? In the world of calculus, we have a set of tools called properties, and the Queen’s Property is one of the most powerful ones for simplifying complex problems in seconds.

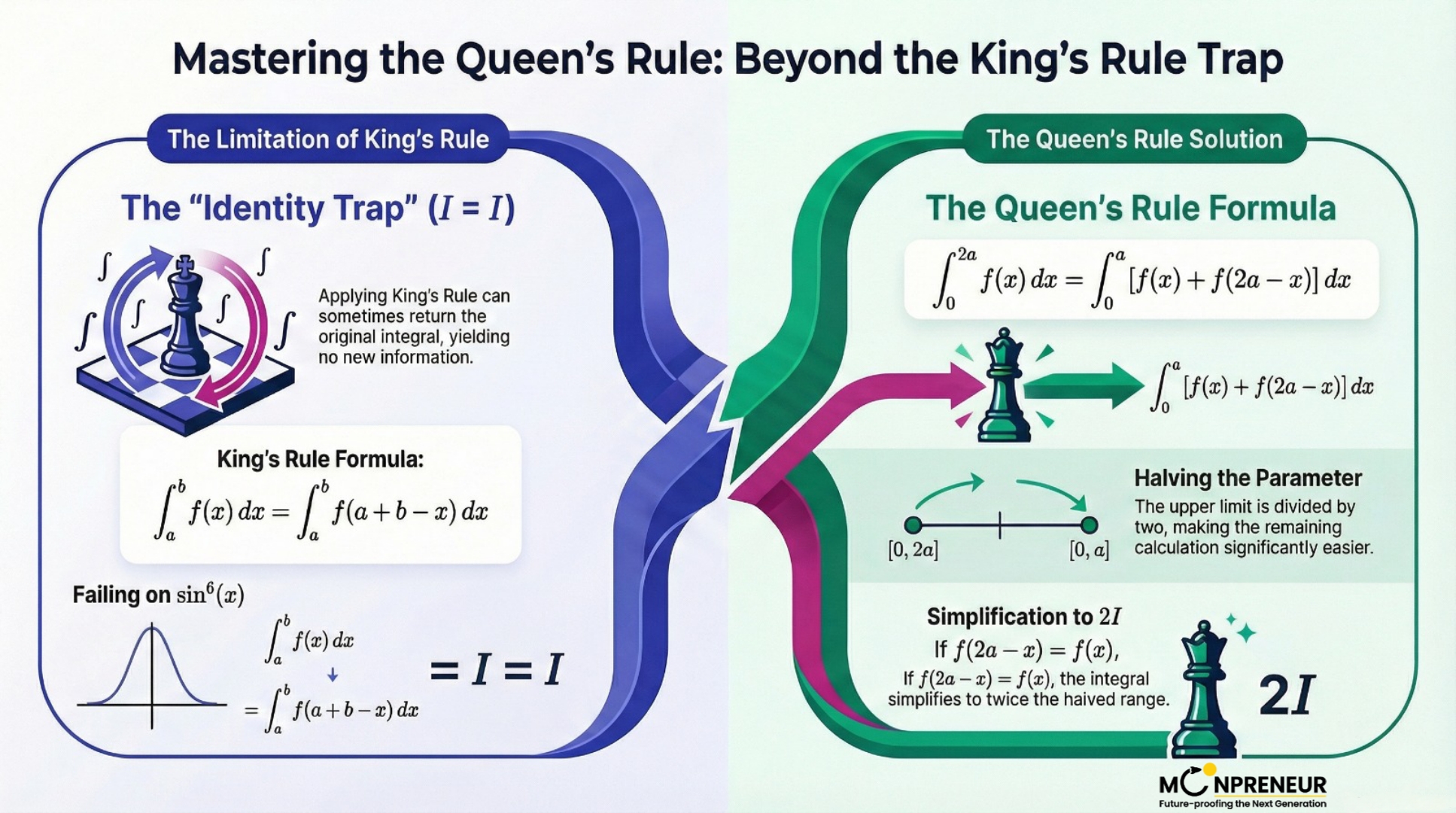
The Problem: When the “King” Fails

In calculus, there is a famous trick called the King’s Rule. It tells us that an integral from a to b is the same even if we replace x with (a + b − x).

It states: \(\displaystyle \int_{b}^{a} f(x)dx = \int_{b}^{a} f(a + b – x)dx\)

But sometimes, the King’s Rule is a dead end. Like for this integral problem: \(\displaystyle \int_{0}^{\pi} \frac{\sin^{6} x}{\sin^{6} x + \cos^{6} x}dx\)

If you try to apply the King’s Rule here, the math loops back on itself. You end up proving that the integral is equal to itself, which doesn’t help you solve for the actual number! This is exactly where most students get frustrated and give up.

Recommended Reading: How to Use King’s Rule in Definite Integrals: Formulas & Solved Examples

The Solution: Queen’s Rule

When the King’s Rule fails to break the loop, the Queen’s Rule steps in to save the day. It’s a property designed to handle integrals where the upper limit (let’s call it 2a) can be split in half.

The formula looks like this: \(\displaystyle \int_{0}^{2a} f(x)dx = \int_{0}^{a} [f(x) + f(2a – x)]dx\)

The Queen’s Rule simplifies definite integrals of the form \(\displaystyle \int_{0}^{2a} f(x)dx\) checking if \(\displaystyle f(2a – x) = f(x)\). It states that if this symmetry holds, the integral becomes \(\displaystyle 2\int_{0}^{a} f(x)dx, \text{ or } 0 \text{ if } f(2a – x) = -f(x)\), allowing easier to evaluate by halving the upper limit. 

Essentially, the Queen’s Rule allows you to cut the integration interval in half (from 0→π down to 0→π/2) while combining the function’s values. While the King’s Property changes the integrand, the Queen’s Property is specifically used to change the limits of integration.

Common Use Cases

This rule is typically applied in two scenarios based on the symmetry of the integrand:

1. If f(2a – x) = f(x): The integral doubles while the upper limit is halved:

\(\displaystyle \int_{0}^{2a} f(x)dx = 2\int_{0}^{a} f(x)dx\)

1. If f(2a – x) = -f(x): The integral evaluates directly to zero:

\(\displaystyle \int_{0}^{2a} f(x)dx = 0\)

Why This is a Game-Changer (Step-by-Step)

1. Identify your limits: In our example, the upper limit is π. So, we set 2a = π, which means a =  π/2.

2. Split and Simplify: Using the Queen’s Rule, the integral becomes a sum of the original function and the function evaluated at (π − x).
3. The Double-Up: In this specific case, the two parts of the function actually end up being identical! This allows us to rewrite the problem as twice the integral from 0 to π/2.
4. The Final Strike: Once the limit is reduced to π/2, you can apply the King’s Rule again. This time, it works perfectly, simplifying the entire fraction down to a simple “1”.

The result? A problem that looked like a nightmare simplifies into a basic calculation, leading to the final answer of π/2.

Example:

Evaluate: \(\displaystyle I = \int_{0}^{\pi} \sin^{2}(x),dx\)

Solution:

Step 1: Identify the components

The integral is in the form \(\displaystyle \int_{0}^{2a} f(x),dx\), where the upper limit 2a = Π. Therefore,a = Π/2. the integrand is \(\displaystyle f(x) = \sin^{2}(x)\).

Step 2: Test the symmetry

We need to check the value of f(2a – x), which is in this case f(Π – x): \(\displaystyle f(\pi – x) = \sin^{2}(\pi – x)\)

Since Sin(Π – x) = Sin(x), it follows that:  \(\displaystyle \sin^{2}(\pi – x) = (\sin x)^{2} = f(x)\)

Because f(Π – x) = f(x), we apply the first case of Queen’s Property

\(\displaystyle \int_{0}^{2a} f(x)\,dx = 2\int_{0}^{a} f(x)\,dx\)

Step 3: Apply the property and solve

By applying the rule, we halve the upper limit and double the integral: \(\displaystyle I = 2\int_{0}^{\pi/2} \sin^{2}(x)\,dx\)

Now, use the identity \(\displaystyle \sin^{2}(x) = \frac{1 – \cos(2x)}{2}\)

The value of integral \(\displaystyle \int_{0}^{\pi} \sin^{2}(x)\,dx\) is Π/2.