If you are preparing for the SAT, you already know that trigonometry can sometimes feel like a whirlwind of formulas to memorize. One of the most famous identities is the Angle Addition Identity: sin(A + B) = sinA cosB + cosA sinB
But what if you didn’t have to just “memorize” it? What if you could see it? Today, we are diving into a visual proof that is so elegant, it turns a complex formula into a simple puzzle of triangles and rectangles. Understanding the logic behind the math is the best way to ensure you never forget it during the high pressure of exam day.
The Secret Weapon: Projections
Before we start the proof, there is one foundational tool you need in your SAT toolkit: Projections.
Imagine a right-angled triangle where the longest side (the hypotenuse) is length x and the angle is θ.
- The side adjacent to the angle is xcosθ.
- The side opposite the angle is xsinθ
You have to master this simple concept—that the sides of a triangle are just “projections” of the hypotenuse—then you can unlock almost any trigonometry problem on the SAT.
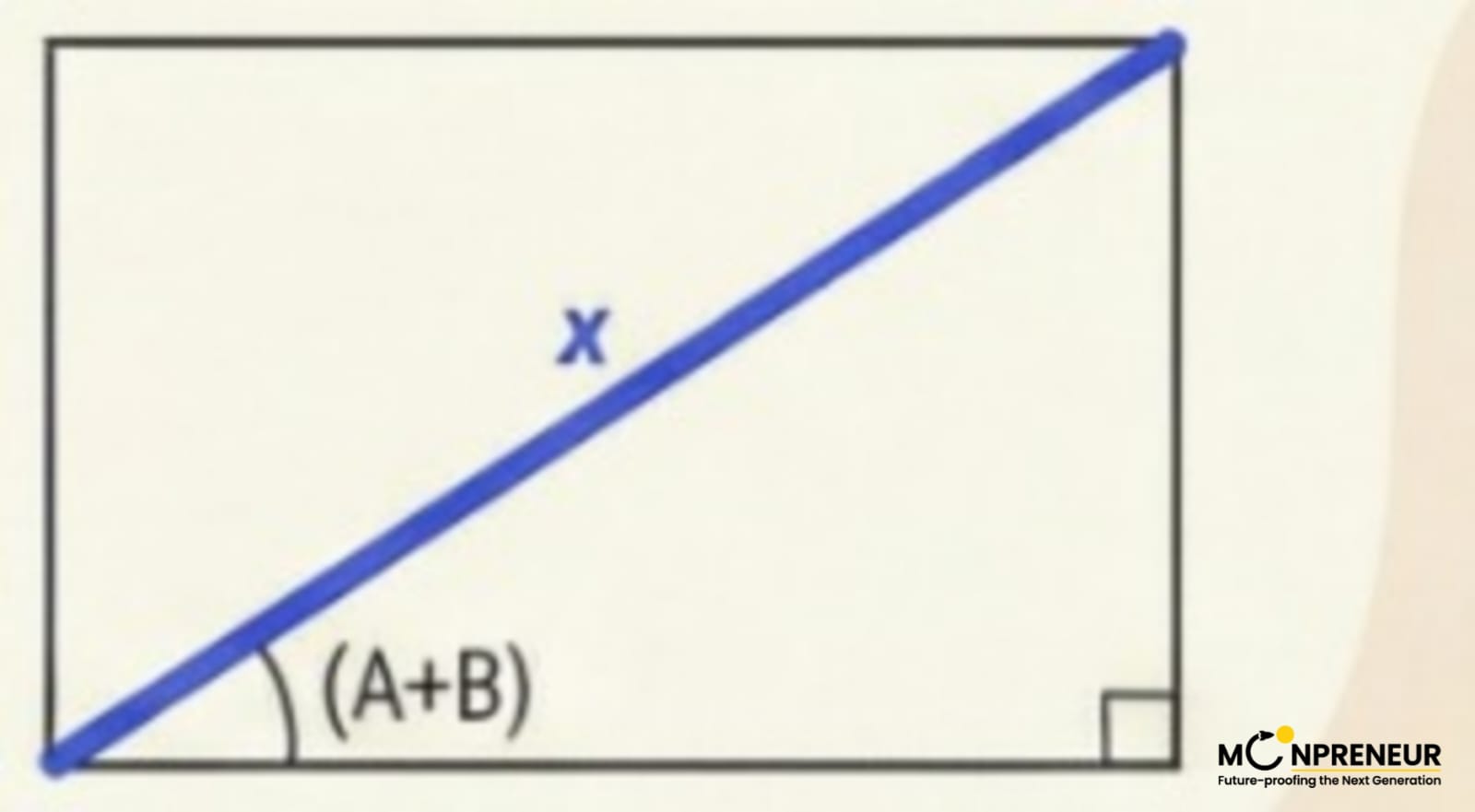
The Setup: One Rectangle, Three Triangles
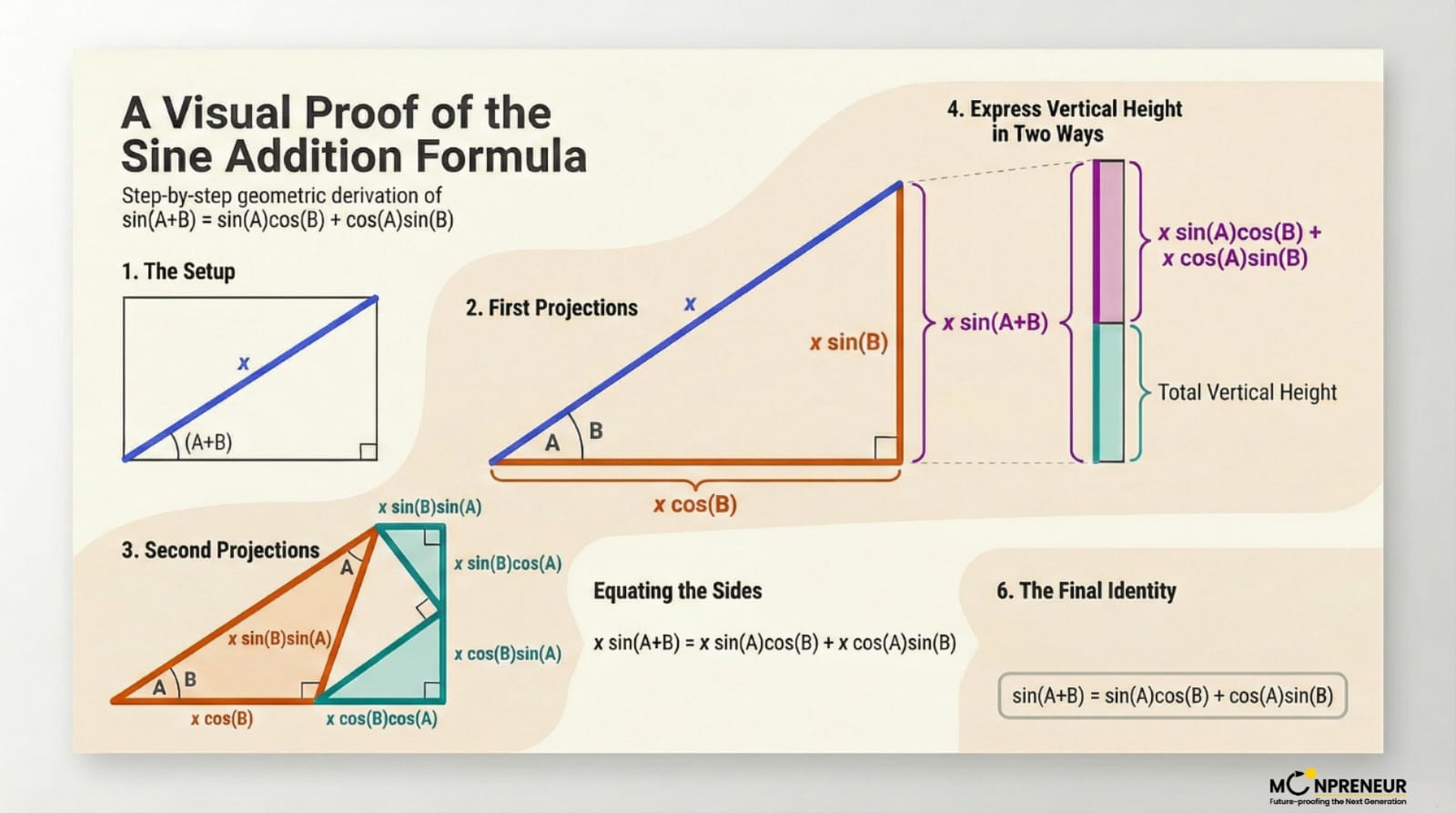
To prove the identity, we start by drawing a rectangle. Inside this rectangle, we draw a line of length x and build a series of right-angled triangles.
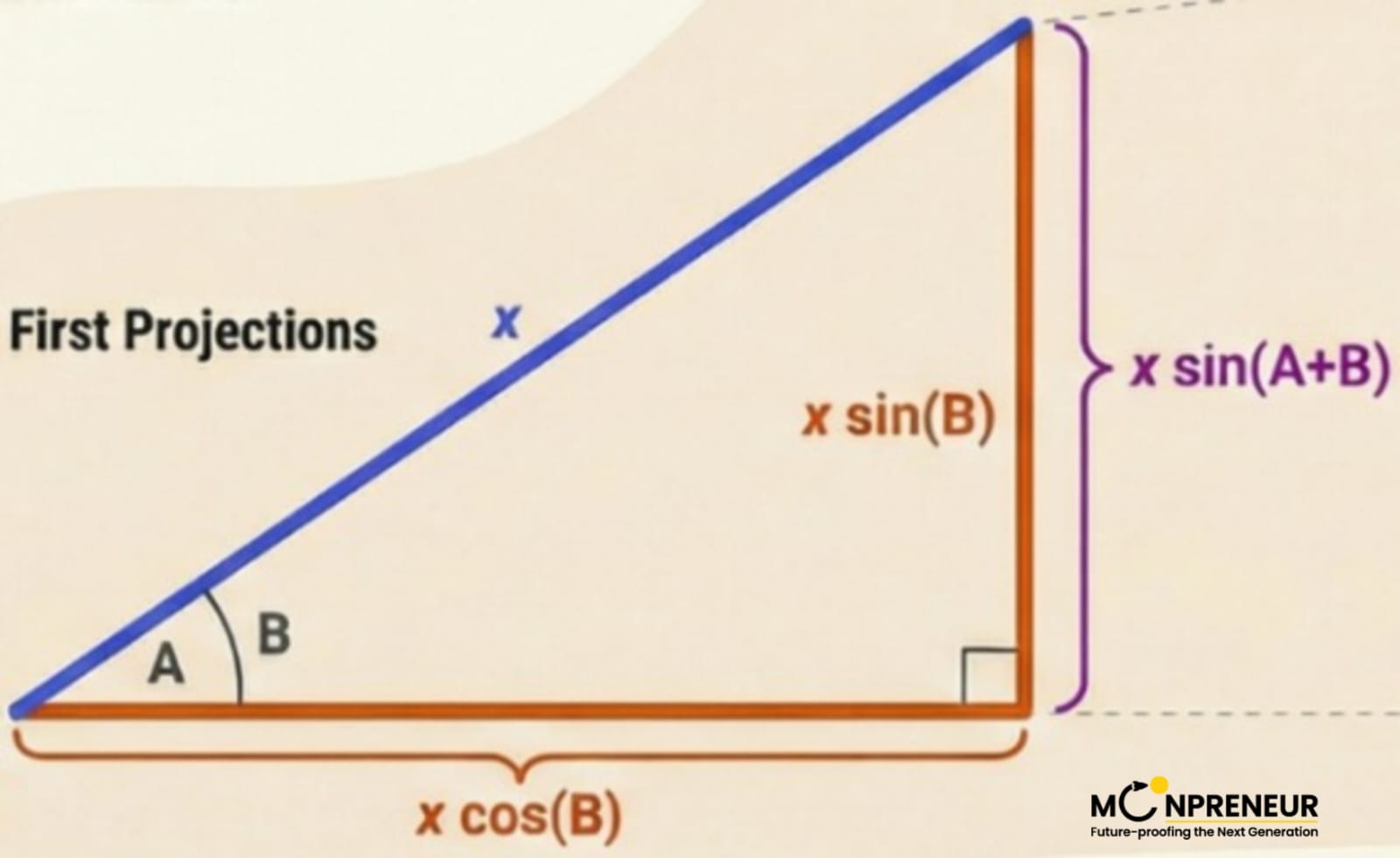
The First Angle (B): We create a triangle where the hypotenuse is x and the angle is B. Based on our projection rule, the base of this triangle is xcosB and the height is xsinB.
- The Second Angle (A): Now, we use that base (xcosB) as the hypotenuse for a new triangle with angle A. The vertical projection (the height) of this new section becomes xcosBsinA.
- The Top Triangle: Now look at the side we labeled xsinB. Through some clever geometry—remembering that the angles in a triangle and on a straight line must sum to 180º.
We can determine that the top angle in this section is also A. This means its vertical projection is xsinBcosA.
Combining it
We’ve carved up the total height of our shape into two segments: xsinAcosB and xcosAsinB.
In the same construction, the total angle formed from our starting point is A+B. Therefore, the entire vertical side of our rectangle can be represented as xsin(A+B).
Because the total height must equal the sum of its parts, we get: xsin(A+B)=xsinAcosB+xcosAsinB.
Now, simply cancel the x from both sides, and you get,
sin(A + B) = sinA cosB + cosA sinB
For a more detailed walkthrough, you can watch this video:
Why is this important for you?
The SAT tests your ability to manipulate triangles and understand the relationships between angles. While you might not be asked to write out a full proof on the test, visualising these projections helps you:
- Move faster: You won’t waste time second-guessing if it’s sinAcosB or sinAsinB.
- Solve complex geometry: Many “Hard” level SAT math questions are just “hidden” versions of these projections
Recommended Reading:
- Solving Exponential Equations Using Recursion: A Step-by-Step Guide
- Linear Equation – One Solution, No Solution and Many Solutions
- Interesting Geometry Problem to Solve For Kids
- Application & Proof of the Sherman-Morrison-Woodbury Identity
- The Geometry Problem That Still Defeats ChatGPT, Gemini, and Grok
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.