We all have seen that one geometry question where we want a faster way to find that one missing side length. If you’ve ever felt like geometry is just a collection of random rules, it’s time to simplify. One of the best theorems in the math section is the Angle Bisector Theorem. In this blog, we will see the proof and its example, too.
What is “Angle Bisector Theorem”?
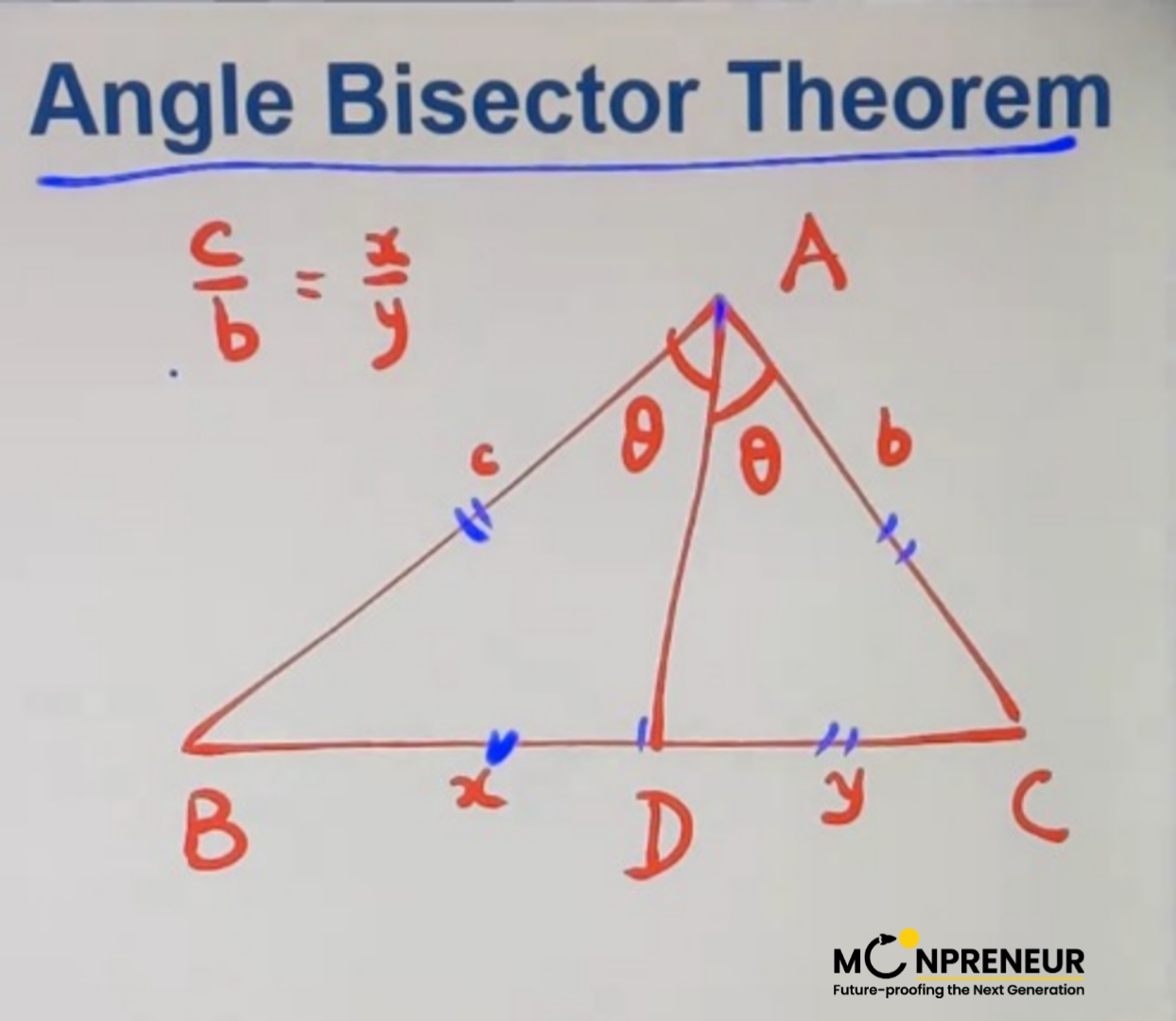
The theorem states that “if you have a triangle and you draw a line that splits one of the angles exactly in half (bisecting it), that line will divide the opposite side of the triangle into two parts. The ratio of those two new segments is exactly the same as the ratio of the other two sides of the triangle
Here, if triangle ABC is divided into two equal triangles ABD and ACD, by line AD, then the ratio \(\displaystyle \frac{BD}{DC} = \frac{AB}{AC}\)
Proof of Angle Bisector Theorem
Statement: The angle bisector of a triangle divides the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides.
Let’s prove this statement.
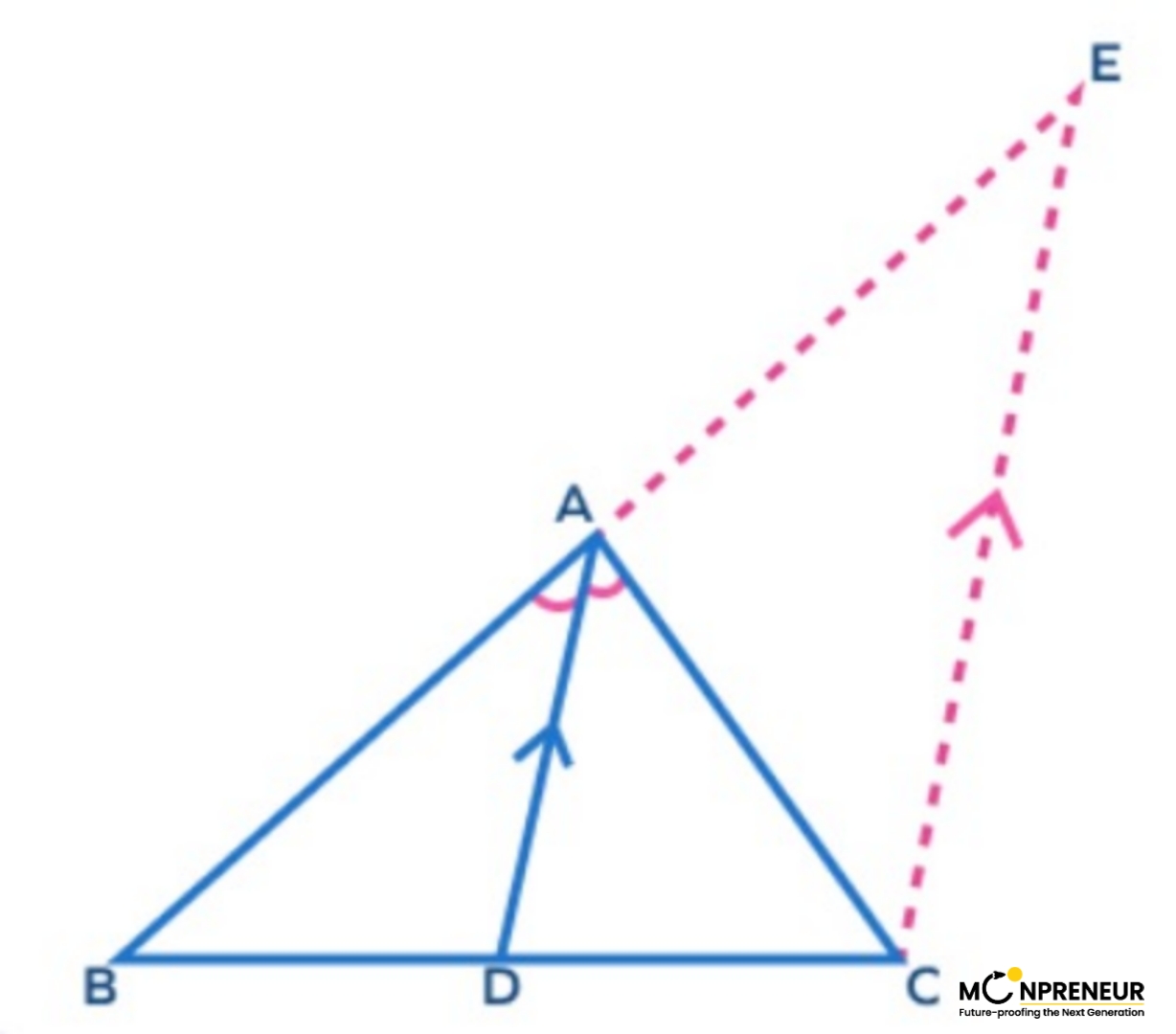
Given: Let us consider triangle ABC, in which AD is the angle bisector of angle BAC, which meets BC at point D.
To prove: \(\displaystyle \frac{BD}{DC} = \frac{AB}{AC}\)
Construction: Draw a ray CE parallel to DA. Extend BA such that it intersects CE at E.
Since CE || DA, AC acts as the transversal.
∠DAC = ∠ACE (alternate interior angles)…(1)
∠BAD = ∠AEC (corresponding angles)……..(2)
As we know that AD is the angle bisector of∠BAC,
∠BAD = ∠DAC…..(3)
From (1), (2) and (3), we have
∠ACE = ∠AEC this implies that triangle ACE is an isosceles triangle.
Therefore, opposite sides of equal angles are equal.
Thus, for triangle ACE, we can write
AE = AC ……..(4)
By the triangle proportionality theorem, if a line parallel to one side of a triangle intersects the other two sides of the triangle, and then the line divides these two sides proportionally.
\(\displaystyle \frac{BD}{DC} = \frac{AB}{BE} \qquad (5)\)From equation (4), we have AE = AC, so on replacing AE by AC in equation (5), we get
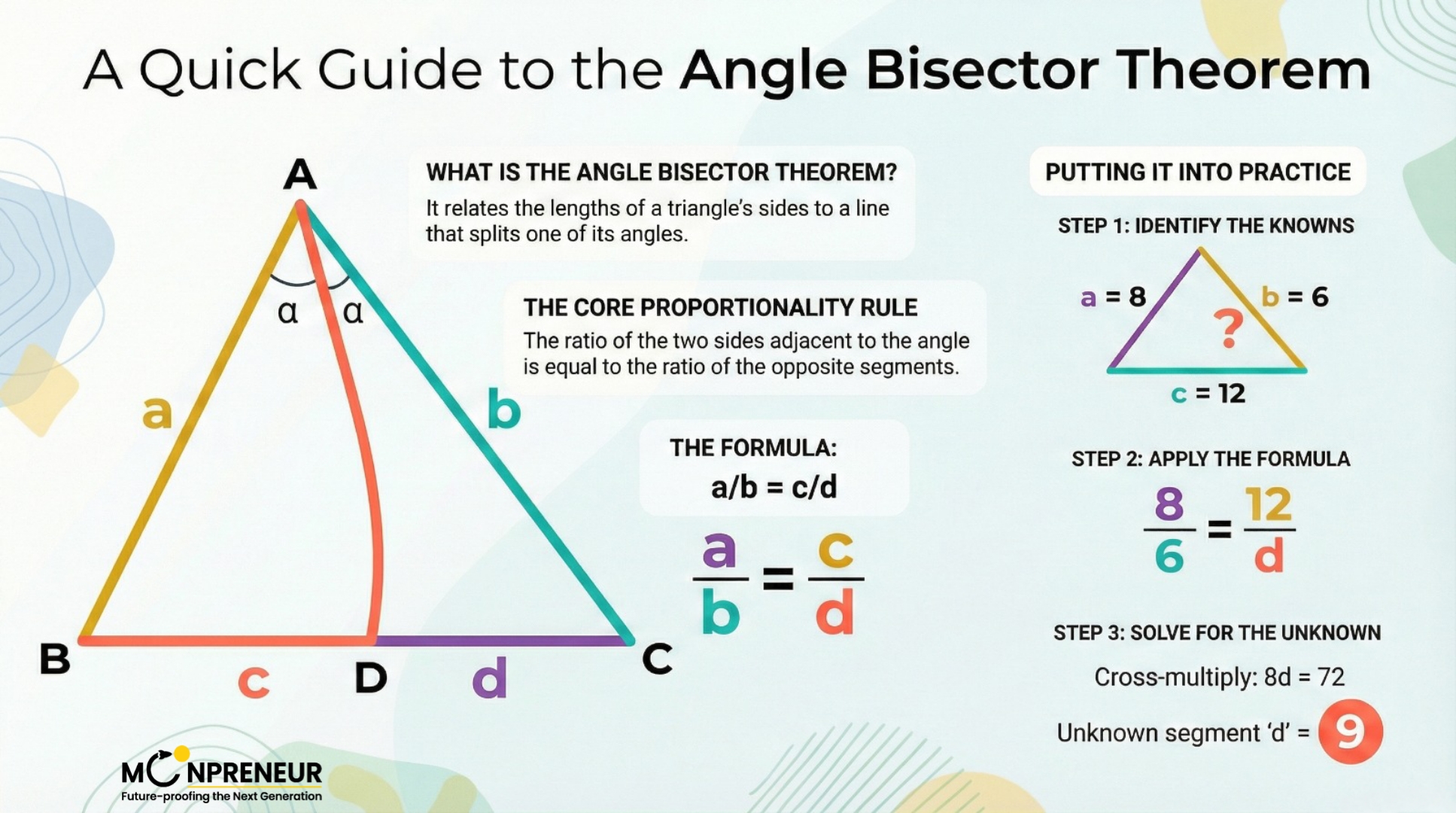
\(\displaystyle \frac{BD}{DC} = \frac{AB}{AC}\)Example of Angle Bisector Theorem
Example 1: Finding the Side Length
- In triangle ABC, the angle bisector of angleA intersects BC at D. If AB = 6cm, AC = 9cm, and BD = 4cm, find the length of DC.
Solution: using the theorem \(\displaystyle \frac{BD}{DC} = \frac{AB}{AC}\)
- \(\displaystyle \frac{4}{DC} = \frac{6}{9}\)
- 6 × DC = 4 × 9
- 6 × DC = 36
- DC = 6 cm.
For a more detailed walkthrough, you can watch this video:
Benefit for SAT Students
The SAT math section isn’t just about what you know; it’s about how fast you can apply it. Instead of using complicated trigonometry or multiple steps of the Pythagorean theorem, the Angle Bisector Theorem allows you to set up a quick cross-multiplication equation and move on to the next question.
Beyond the Formulas
It’s easy to get overwhelmed by complex questions in the SAT, but remember that these exams are just as much about strategy as they are about numbers. Learning tricks like graphing linear functions in seconds or quick table-writing methods can turn a daunting 800-point goal into a series of manageable, small wins
Recommended Reading:
- How to Derive and Use the Quadratic Formula (With Examples)
Application & Proof of the Sherman-Morrison-Woodbury Identity
- Linear Equation – One Solution, No Solution, and Many Solutions
- Solving Exponential Equations Using Recursion: A Step-by-Step Guide
- Condition of Tangency for a Parabola: Formula and Derivation
- How to Prove the Law of Sines: Easy Guide with Diagrams
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.