How to Prove the Law of Sines: Complete Guide with Diagrams

When you are staring at a geometry problem on a practice SAT, wondering why the triangle in front of you isn’t a nice, simple right triangle, when the Pythagorean theorem fails you, it’s easy to feel stuck. But there is a powerful tool that works for any triangle: the Law of Sines.

In this blog, we will deep dive into the concept of the Law of Sines.

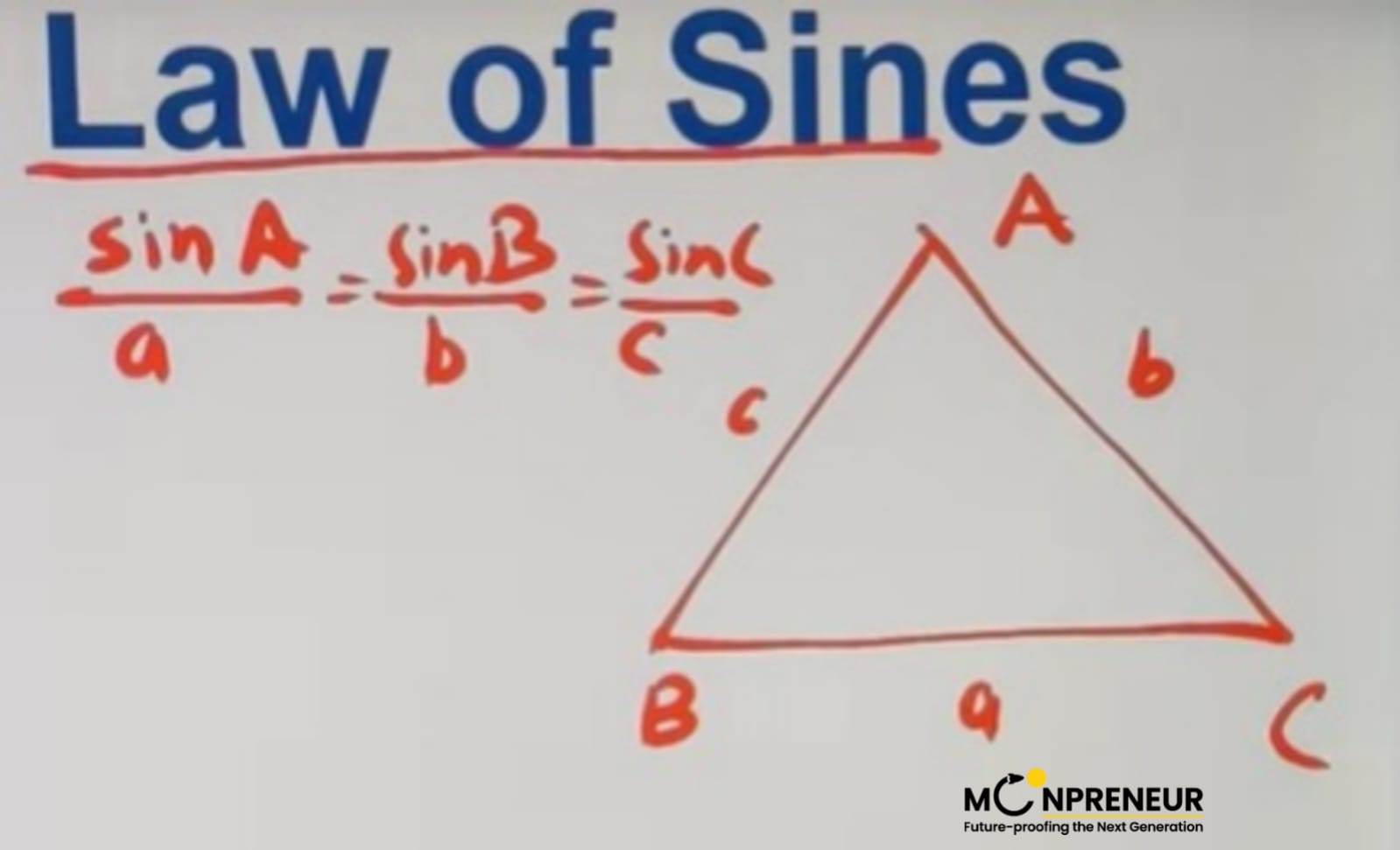
The Law of Sines:

The Formula:

The sine rule proof shows that for any triangle (sides a, b, c; opposite angles A, B, C) , the ratio of a side to the sine of its opposite angle is constant: \(\displaystyle \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\)

Now, we will deep dive to see how the Law of Sines originated and got its form.

The Proof:

1. Setup: Consider a triangle ABC with sides a, b, and c, opposite angles A, B, and C, respectively.
2. Construction: Draw an altitude (height, h) from vertex C to the side AB, meeting at point D. This creates two right-angle triangles, ADC and BDC.
3. Apply Sine in triangle ADC: \(\displaystyle \sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{b}\)
   Rearrange to solve for \(\displaystyle h = b \sin A\)
   
4. Apply Sin in triangle BDC:  \(\displaystyle \sin B = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{a}\)
   Rearrange to solve for h: h = a Sin B
5. Equate the expressions for h: Since both expressions are equal for h, we can set them equal: b Sin A = a Sin B
6. Rearrange to get the rule: Divide both sides to isolate the ratios:  \(\displaystyle \frac{b \sin A}{ab} = \frac{a \sin B}{ab}\)
   \(\displaystyle \frac{\sin A}{a} = \frac{\sin B}{b}\)
7. Extend to the third side: by drawing the altitude from another vertex (e.g., from B to AC), the same process proves that \(\displaystyle \frac{b}{\sin B} = \frac{c}{\sin C}\)
   
8. Conclusion: Combining all these, we get: \(\displaystyle \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\)

For a more detailed walkthrough, you can watch this video: