Have you ever felt that you cannot solve a complex geometry problem? You aren’t alone. In fact, even the most advanced AI models like ChatGPT, Gemini, and Grok often struggle to solve certain intricate spatial puzzles correctly. Today, in this blog, we will see a geometry problem that requires exactly the kind of logical thinking that will help you ace the SAT.
The Challenge: Finding the Hidden Area
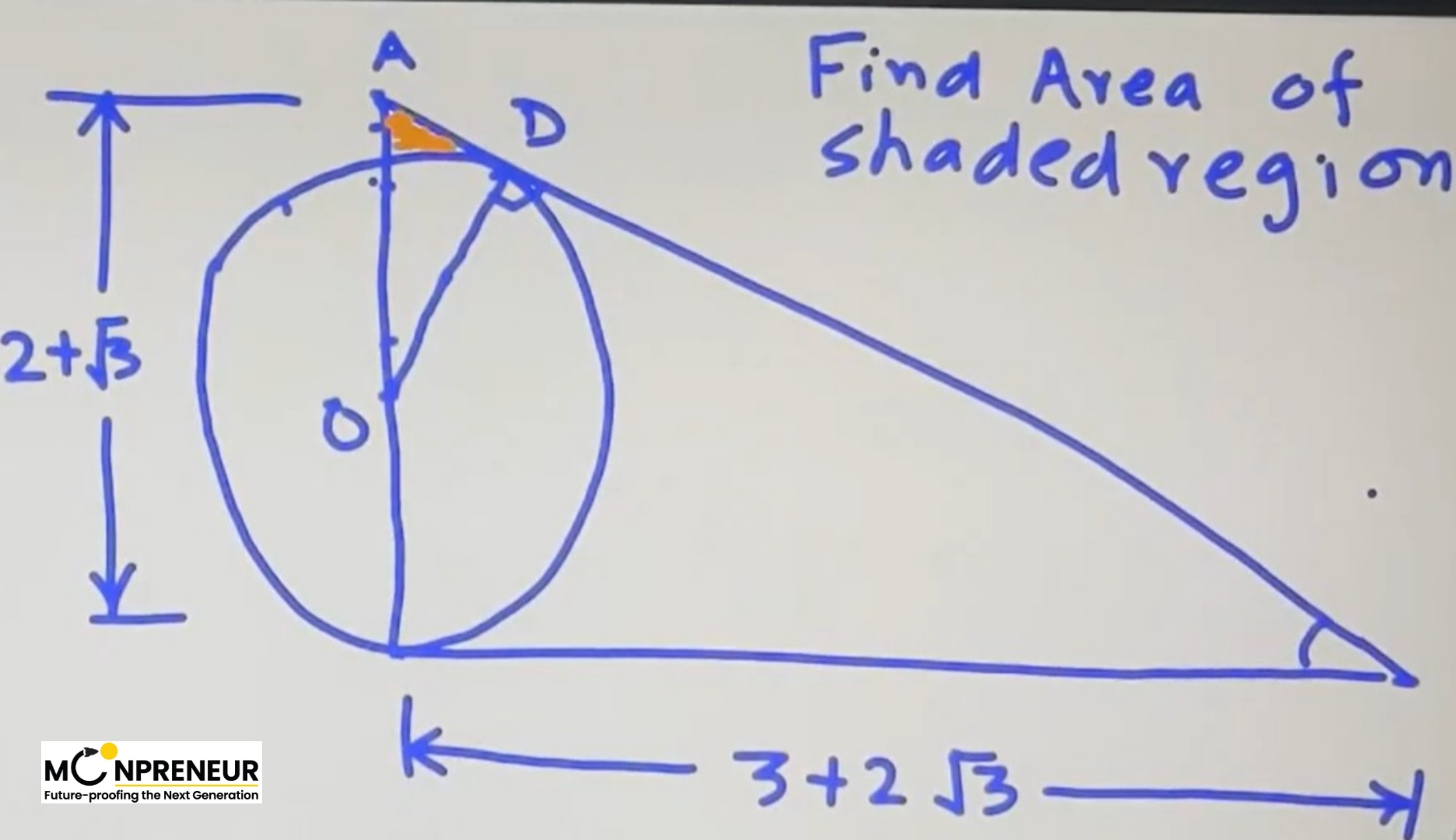
The problem presents us with a right-angled triangle containing a circle that touches the hypotenuse. Our mission is to find the area of a specific shaded region.
To crack this, we need a clear strategy.
The shaded region is found by taking the area of a smaller triangle (ADO) and subtracting the area of the circular sector (the arc) that overlaps it. To do this, we first need to find two critical pieces of information: the radius (r) of the circle and the internal angle (θ).
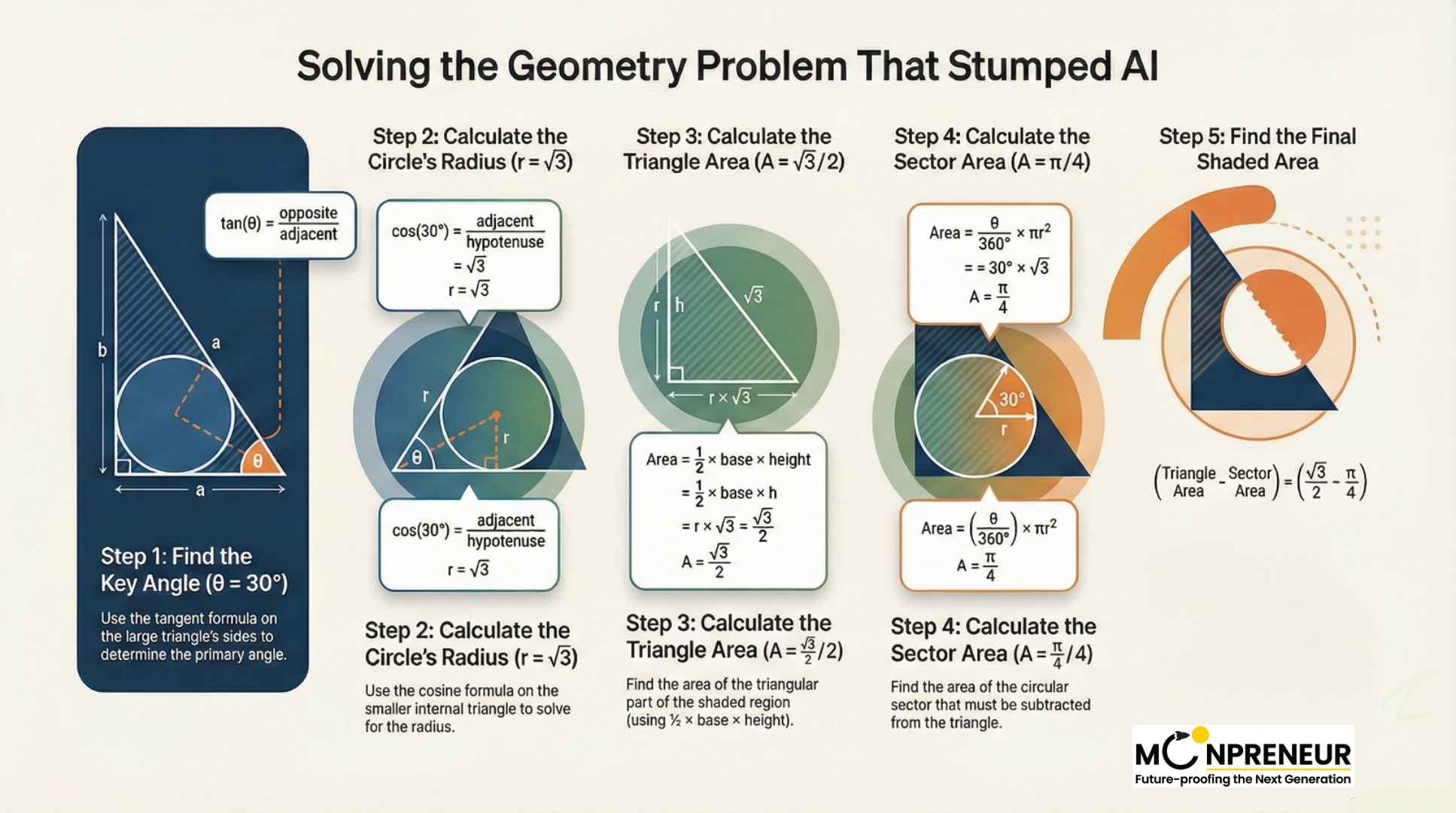
Step 1: The Power of Tangents
In many SAT problems, you are given side lengths that look messy. In this case, the sides are 2 + √3 and 3 + 2√3 .
By setting up a tangent ratio—tan(θ) = opposite/adjacent—we can find the angle.
By multiplying the numerator and denominator by the conjugate to simplify the fraction, the maths beautifully unfolds to show that tan(θ) = 1/√3 . This tells us that θ is 30º
Recognizing these special right triangle ratios (30−60−90) is really important.
Step 2: Solving for the Radius
Next, we need the radius (r). By using the cosine of 30º, we can create an identity involving r and the side lengths. Through some algebraic simplification—again using conjugates to keep things tidy—we find that the radius simplifies to a very clean √3.
Step 3: Calculating the Shaded Area
Now that we have our measurements, we can find the two areas:
- The Circular Sector: Since the angle is 30 degrees, this section is 30/360 (or 1/12) of the total circle. Using the formula Area = πr², we find that this area is π/4.
- The Triangle (ADO): Using the formula Area = \(\displaystyle \frac{1}{2} \times \text{base} \times \text{height}\) we determine the base is 2 and the height is √3/2. This gives us a triangle area of √3/2.
- The Final Answer: By subtracting the sector from the triangle, the shaded region equals √3/2 – π/4 .
For a more detailed walkthrough, you can watch this video:
Why This is important for Your SAT
This problem is a perfect workout for your brain because it combines trigonometry, circle properties, and algebraic simplification. While an AI might get lost in the steps, you can succeed by breaking the problem down into smaller, manageable parts.
Recommended Reading:
- How to Derive and Use the Quadratic Formula (With Examples)
Application & Proof of the Sherman-Morrison-Woodbury Identity
- Linear Equation – One Solution, No Solution and Many Solutions
- Solving Exponential Equations Using Recursion: A Step-by-Step Guide
Want to excite your child about math and sharpen their math skills? Moonpreneur’s online math curriculum is unique as it helps children understand math skills through hands-on lessons, assists them in building real-life applications, and excites them to learn math.
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.