In mathematics, understanding the rise over run formula is essential for learning about slopes of lines in geometry and algebra. The slope helps describe how steep a line is, and the rise over run method makes it easy to calculate. This concept is widely used in graphing equations, architecture, engineering, and everyday problem-solving.
What is the Rise Over Run Formula?
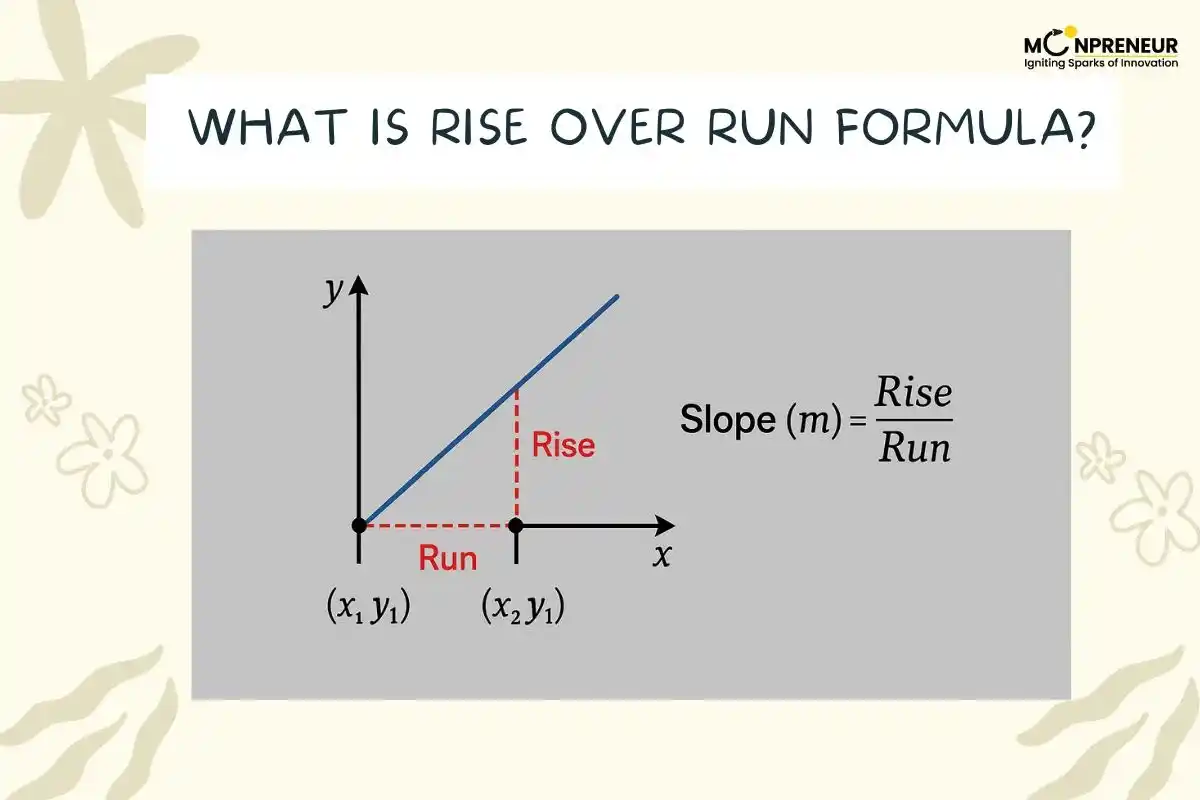
The rise over run formula is used to calculate the slope of a line. It measures how much a line goes up or down (rise) compared to how much it moves sideways (run).
Formula: \(\text{Slope } (m) = \frac{\text{Rise}}{\text{Run}}\)
Where:
– Rise = Change in vertical direction (difference in y-coordinates)
– Run = Change in horizontal direction (difference in x-coordinates)
Step-by-Step Example
Suppose you have two points on a line: (x₁, y₁) and (x₂, y₂).
The slope (m) is given by: \(m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}\)
Example:
For points (2, 3) and (6, 7):
\(m = \frac{7 – 3}{6 – 2} = \frac{4}{4} = 1\)
So, the slope of the line is 1.
Real-Life Applications of Rise Over Run
– Architecture: Used in designing ramps and roofs.
– Road Construction: Determines slope of roads and railways.
– Algebra & Geometry: Helps in graphing linear equations.
– Engineering: Calculates slopes for drainage systems and bridges.
Key Points to Remember
– A positive slope means the line goes upward from left to right.
– A negative slope means the line goes downward from left to right.
– A slope of 0 means the line is horizontal.
– An undefined slope means the line is vertical.
Some Examples of Rise Over Run Formula
Example 1:
Find the slope of the line passing through the points (1, 2) and (4, 8).
Solution:
\(m = \frac{8 – 2}{4 – 1} = \frac{6}{3} = 2\)
So, the slope is 2.
Example 2:
Find the slope of the line passing through the points (3, 5) and (7, 5).
Solution:
\(m = \frac{5 – 5}{7 – 3} = \frac{0}{4} = 0\)
So, the slope is 0 (horizontal line).
Example 3:
Find the slope of the line passing through the points (6, 2) and (6, 9).
Solution:
\(m = \frac{9 – 2}{6 – 6} = \frac{7}{0}\)
The slope is undefined (vertical line).
Conclusion
The rise over run formula is a simple yet powerful mathematical concept that explains the slope of a line. By calculating the change in vertical (rise) and horizontal (run), you can easily determine the steepness and direction of any line. Whether you’re solving math
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle
















