What is a Scalene Triangle?
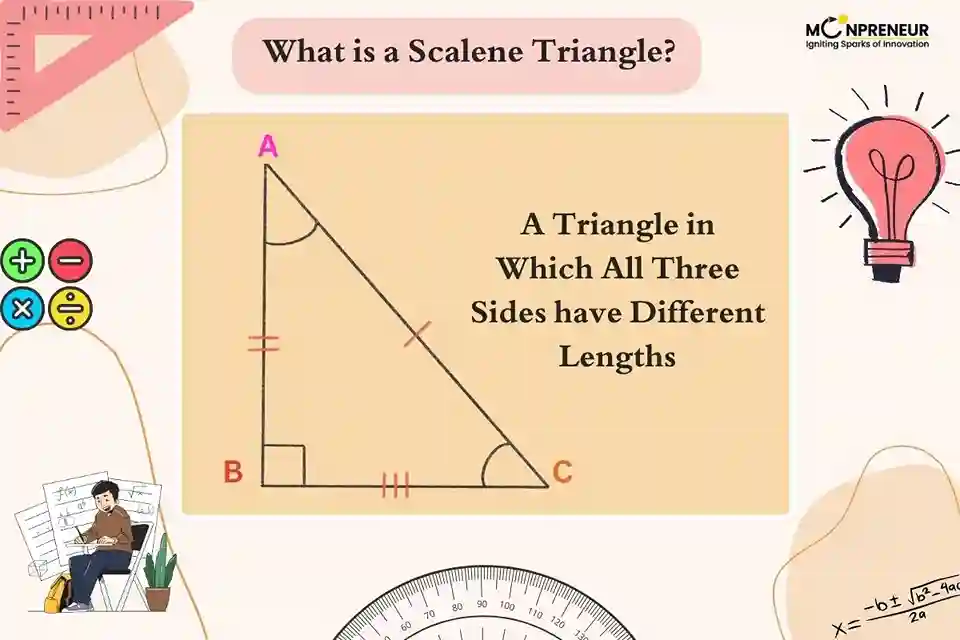
When learning about triangles in geometry, one important category to understand is the scalene triangle. Unlike other types of triangles, a scalene triangle stands out for having no equal sides or angles. In this blog, we’ll explore what a scalene triangle is, its properties, real-life examples, and why understanding it is important for students.
Definition: What is a Scalene Triangle?
A scalene triangle is a type of triangle where all three sides are of different lengths, and each angle is different as well. This means:
- No two sides are equal.
- No two angles are the same.
- It does not have any line of symmetry.
Properties of a Scalene Triangle
Understanding the properties of a scalene triangle can help you easily identify and solve problems involving them:
- All sides are unequal
- All angles are unequal
- The sum of all interior angles is always 180°
- It can be acute, right, or obtuse
- It has no line of symmetry
Types of Scalene Triangles
Yes, a scalene triangle can fall into other categories based on angles:
- 🔹 Acute Scalene Triangle: All angles are less than 90°
- 🔹 Right Scalene Triangle: One angle is exactly 90°
- 🔹 Obtuse Scalene Triangle: One angle is more than 90°
Scalene Triangle Example
Imagine a triangle with side lengths of 5 cm, 6 cm, and 7 cm. None of the sides are equal, and the angles are all different too. This is a perfect example of a scalene triangle:
How to Identify a Scalene Triangle
You can recognize a scalene triangle by checking:
- Are all three sides different? ✔
- Are all three angles different? ✔
If the answer is yes to both, you’re looking at a scalene triangle!
Real-Life Examples of Scalene Triangles
Scalene triangles appear in real life more often than you think!
- Construction: Support beams and trusses in buildings
- Art & Design: Abstract patterns and shapes
- Road signs: Some warning signs use irregular triangle shapes
Area of a Scalene Triangle
To find the area of a scalene triangle, you can use Heron’s Formula:
Let the sides be a, b, and c
Step 1: Find the semi-perimeter (s):
s = (a + b + c) / 2
Step 2: Apply Heron’s Formula to find the area:
Area = √[s × (s − a) × (s − b) × (s − c)]
Why Should Students Learn About Scalene Triangles?
Learning about different types of triangles, especially scalene ones, helps students:
- Improve spatial thinking
- Understand geometry concepts better
- Prepare for math exams and competitive tests
- Recognize triangle types in real-life scenarios
Quick Recap: Scalene Triangle Facts
| Feature | Scalene Triangle |
|---|---|
| Sides | All sides are different |
| Angles | All angles are different |
| Symmetry | No line of symmetry |
| Area | Use Heron’s formula |
| Can be | Acute, right, or obtuse |
🌟 Final Thoughts
A scalene triangle is a fundamental concept in geometry that helps students understand the diversity of triangle shapes. From basic math classes to real-world applications in architecture and design, knowing how to identify and work with scalene triangles is a must-have skill. So, next time you see a triangle with all different sides—now you know, it’s scalene!
Want to spark your child’s interest in math and boost their skills? Moonpreneur’s online math curriculum stands out because it engages kids with hands-on lessons, helps them apply math in real-life situations, and makes learning math exciting!
You can opt for our Advanced Math or Vedic Math+Mental Math courses. Our Math Quiz for grades 3rd, 4th, 5th, and 6th helps in further exciting and engaging in mathematics with hands-on lessons.
Related Blogs:
How to Teach Adjacent Angles to Kids | Simple & Fun Guide
What are Congruent Angles?
Understanding Alternate Interior Angles
What is the Area of Trapezoid?
What is the Area of Parallelogram?
Understanding the Geometry Regents: A Comprehensive Guide
How to Prepare for the Geometry Regents: Study Plans & Practice
The Art of Geometry: How to Draw an Equilateral Triangle Inside a Circle
















