Update: This article was last updated on 22nd November 2024 to reflect the accuracy and up-to-date information on the page.
Triangles are fundamental geometric shapes, forming the building blocks for more complex polygons and shapes. One of the critical aspects of a triangle is its vertices of a triangle – those corner points where the sides of the triangle meet. Understanding the vertices of a triangle is crucial for basic geometry, advanced mathematics, and applications in various fields like computer graphics, physics, and engineering. This blog will delve into triangle vertices with examples to deepen our understanding
What are Triangle Vertices?
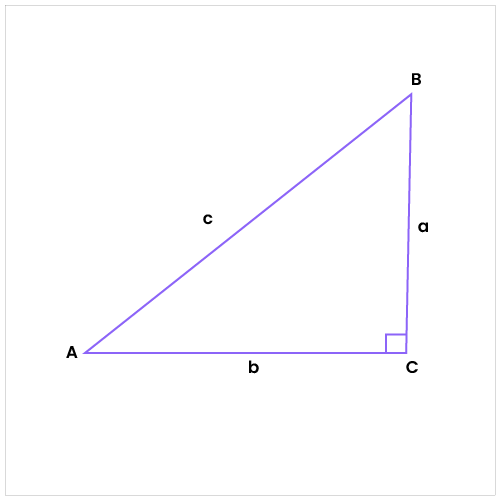
Vertices (singular: vertex) are the points where the sides of a triangle intersect. Every triangle has three vertices, and these points collectively define the shape and properties of the triangle.
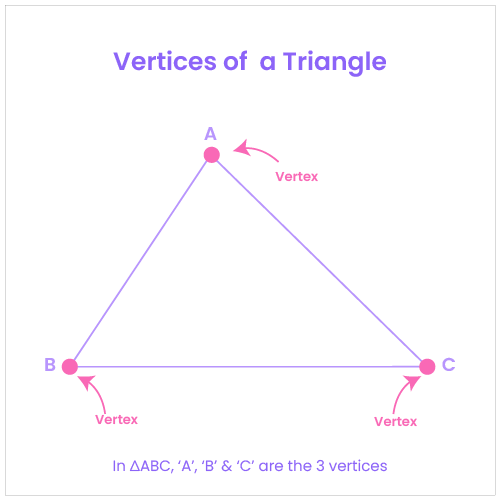
The vertices are typically named using capital letters A, B, and C.
Example 1:
Consider the following triangle:
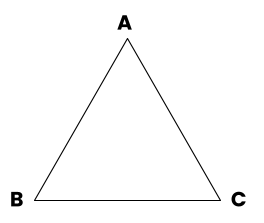
In this triangle, the vertices are labeled A, B, and C. The sides are AB, BC, and CA.
Properties and Characteristics
Understanding the vertices of a triangle opens up a world of insights into the triangle’s properties and characteristics.
Triangle Types Based on Angles:
Acute Triangle: All angles are less than 90 degrees.
Obtuse Triangle: One angle is greater than 90 degrees.
Right Triangle: One angle is precisely 90 degrees.
Triangle Types Based on Sides:
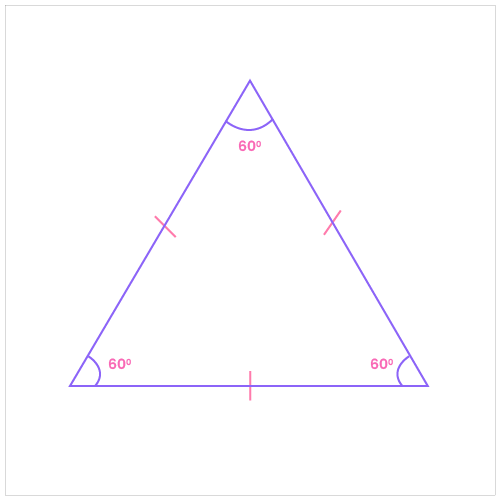
Equilateral Triangle: All sides are of equal length.
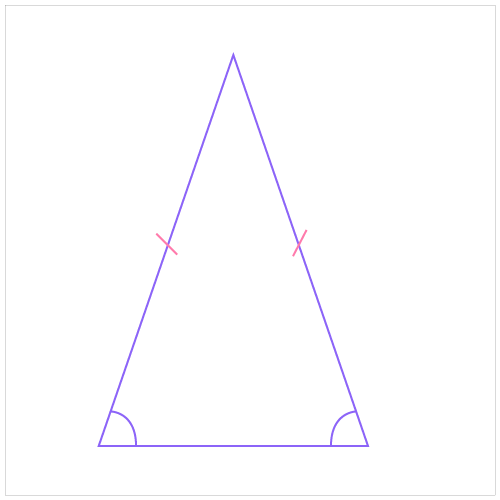
Isosceles Triangle: Two sides are of equal length.
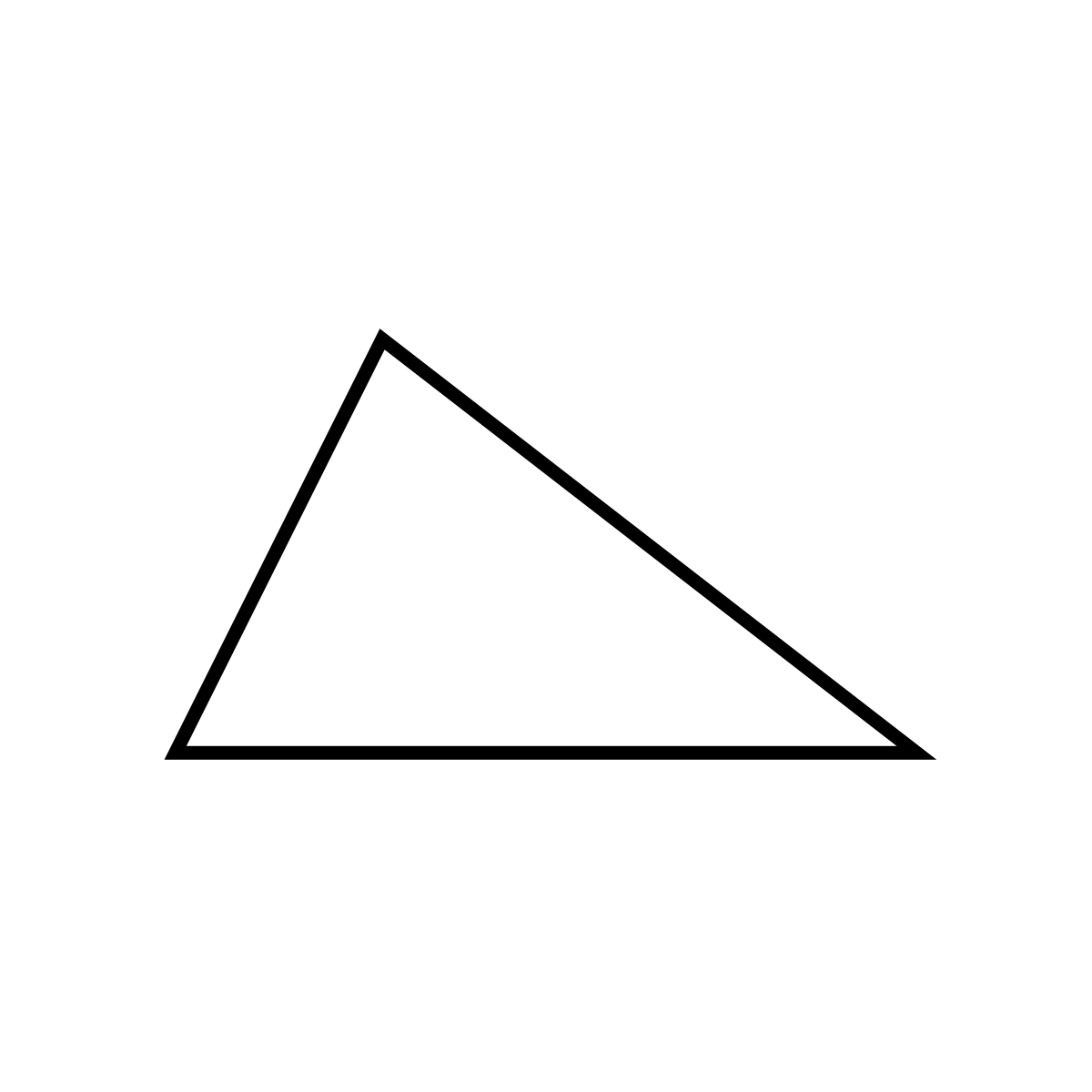
Scalene Triangle: All sides have different lengths.
Angle Sum Property:
The sum of the angles in any triangle always equals 180 degrees. This property is a consequence of a straight line measuring 180 degrees.
Example 2:
Consider a triangle with angle measurements: ∠A = 50°, ∠B = 70°, and ∠C = 60°.
Using the angle sum property, we can verify that:
50° + 70° + 60° = 180°
Thus, the angles satisfy the angle sum property, confirming that they form a triangle.
Recommended Reading: Understanding Axis of Symmetry
Coordinate Geometry and Triangle Vertices
Triangle vertices can also be represented using coordinate geometry. If you know the coordinates of the three vertices, you can determine various properties of the triangle, such as its area, perimeter, and orientation.
Example 3:
Consider a triangle with vertices of a triangle labeled as A, B, and C. The angle measurements are: ∠A = 40°, ∠B = 60°, and ∠C = 80°.
Using the angle sum property, we can verify that:
40° + 60° + 80° = 180°
Thus, the angles satisfy the angle sum property, confirming that these vertices of a triangle form a valid triangle.
Example 4:
Given the vertices A(2, 3), B(5, 7), and C(8, 2), you can calculate the lengths of the sides AB, BC, and CA using the distance formula.
Furthermore, you can find the area of the triangle using methods like the Shoelace Formula or by treating it as half the area of a parallelogram formed by the vectors AB and AC.
Real-World Applications
Understanding triangle vertices is essential in various fields:
Computer Graphics
Vertices play a crucial role in defining the geometry of shapes in 3D computer graphics.
Engineering
We use triangles in finite element analysis to model complex structures. Each vertex of a triangle plays a crucial role in defining the shape and orientation of the element, ensuring accurate calculations and simulations.
Physics
In physics simulations, a vertex of a triangle plays a critical role as it represents a corner point that defines the shape and orientation of the triangle. Triangles can represent facets of objects, aiding in simulations of natural phenomena.
Navigation
Triangles formed by landmarks and positions are used in trigonometric methods for navigation and surveying.
The vertex of a triangle is one of the three corner points where two sides of the triangle meet. Each triangle has three vertices that define its shape and structure.
Triangle vertices are not just points on a shape. They are fundamental in geometry, playing a key role in determining the angles, sides, and overall properties of the triangle. This makes them crucial for calculations in areas like coordinate geometry and finite element analysis.
Understanding the vertex triangle is not just a theoretical concept but a practical necessity. Each vertex provides a reference point for analyzing forces, structural integrity, and design in fields like physics, computer graphics, and engineering.
Conclusion
Triangle vertices are not just points on a shape; they unlock a wealth of geometric and mathematical knowledge.
From defining basic triangle types to enabling advanced calculations in various fields, vertices play a vital role. By understanding triangle vertices, we gain insight into the intricate world of geometry and its practical applications.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!













